题目内容
 如图,有长20m的铁丝网,若一边靠墙围成3个大小相同,紧紧相接的长方形,问每个小长方形的长和宽各是多少时,三个长方形的总面积最大?并求最大面积.
如图,有长20m的铁丝网,若一边靠墙围成3个大小相同,紧紧相接的长方形,问每个小长方形的长和宽各是多少时,三个长方形的总面积最大?并求最大面积.
分析:首先设出每个小长方形的长和宽分别为x,y,然后根据长方形的周长和面积公式分别列等式,建立一元二次函数,求最值即可.
解答:解:设每个小长方形的长和宽分别为x,y
则3x+4y=20,y=
(20-3x)
∴三个长方形的总面积:
S=3xy=3x×
(20-3x)
∴S=-
x2+15x
=-
(x2-
x)
=-
(x-
)2+25
又∵x>0,y=
(20-3x)>0
∴0<x<
∴x=
时,Smax=25,
此时y=
答:每个小长方形的长和宽分别为
,
时,三个长方形的总面积最大为25
则3x+4y=20,y=
| 1 |
| 4 |
∴三个长方形的总面积:
S=3xy=3x×
| 1 |
| 4 |
∴S=-
| 9 |
| 4 |
=-
| 9 |
| 4 |
| 20 |
| 3 |
=-
| 9 |
| 4 |
| 10 |
| 3 |
又∵x>0,y=
| 1 |
| 4 |
∴0<x<
| 20 |
| 3 |
∴x=
| 10 |
| 3 |
此时y=
| 5 |
| 2 |
答:每个小长方形的长和宽分别为
| 10 |
| 3 |
| 5 |
| 2 |
点评:本题考查函数模型的选择与应用,通过对实际问题的分析,抽象出数学模型,建立一元二次函数求解,属于基础题.

练习册系列答案
相关题目
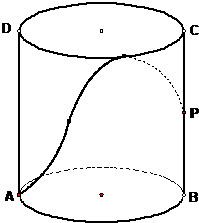 如图,有一圆柱形的开口容器(下表面密封),其轴截面是边长为2的正方形,P是BC中点,现有一只蚂蚁位于外壁A处,内壁P处有一米粒,则这只蚂蚁取得米粒所需经过的最短路程为
如图,有一圆柱形的开口容器(下表面密封),其轴截面是边长为2的正方形,P是BC中点,现有一只蚂蚁位于外壁A处,内壁P处有一米粒,则这只蚂蚁取得米粒所需经过的最短路程为
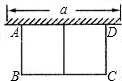 如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为Xm,面积为Sm2,
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为Xm,面积为Sm2,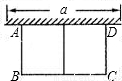 如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为Xm,面积为Sm2,
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为Xm,面积为Sm2, 如图,有长20m的铁丝网,若一边靠墙围成3个大小相同,紧紧相接的长方形,问每个小长方形的长和宽各是多少时,三个长方形的总面积最大?并求最大面积.
如图,有长20m的铁丝网,若一边靠墙围成3个大小相同,紧紧相接的长方形,问每个小长方形的长和宽各是多少时,三个长方形的总面积最大?并求最大面积.