题目内容
【题目】如图，三棱柱
的各棱长均为2，侧面
底面
，侧棱
与底面所成的角为
．
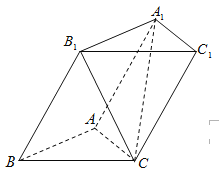
（Ⅰ）求直线
与底面所成的角；
（Ⅱ）在线段
上是否存在点
，使得平面
平面
？若存在，求出
的长；若不存在，请说明理由．
【答案】（1）
；（2）
。
【解析】
试题（1）根据题意建立空间直角坐标系，然后表示平面的法向量和直线的斜向量，进而利用向量的夹角公式得到线面角的求解。
（2）假设存在点满足题意，然后利用向量的垂直关系，得到点的坐标。
解：（1）
作
于
，
∵侧面
平面
，
则
,
,
,
,
,
∴
,又底面的法向量
…4分
设直线
与底面所成的角为
，则
,∴
所以，直线与底面所成的角为
． …6分
（2）设在线段
上存在点
，设
=
，
,则
…7分
设平面
的法向量
令
…9分
设平面
的法向量
令
…10分
要使平面
平面，则
…12分
练习册系列答案
习题精选系列答案
相关题目
【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费
（单位：万元）对年销售量
（单位：
）的影响，对近
年的年宣传费
和年销售量
作了初步统计和处理，得到的数据如下：
年宣传费 |
|
|
|
|
年销售量 |
|
|
|
|
，
.
（1）在给定的坐标系中画出表中数据的散点图；
（2）求出
关于的线性回归方程
；
（3）若公司计划下一年度投入宣传费
万元，试预测年销售量的值.
参考公式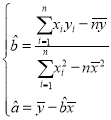
【题目】某公司为了解用户对其产品的满意度，从某地区随机调查了100个用户，得到用户对产品的满意度评分频率分布表如下：
组别 | 分组 | 频数 | 频率 |
第一组 |
| 10 | 0.1 |
第二组 |
| 20 | 0.2 |
第三组 |
| 40 | 0.4 |
第四组 |
| 25 | 0.25 |
第五组 |
| 5 | 0.05 |
合计 | 100 | 1 |
（1）根据上面的频率分布表，估计该地区用户对产品的满意度评分超过70分的概率；
（2）请由频率分布表中数据计算众数、中位数，平均数，根据样本估计总体的思想，若平均分低于75分，视为不满意.判断该地区用户对产品是否满意？