题目内容
已知函数 .
.
(1)若 ,求
,求 在
在 处的切线方程;
处的切线方程;
(2)若 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
【答案】
(1)故曲线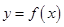 在
在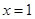 处的切线方程为
处的切线方程为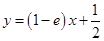 ;(2)
;(2)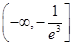 .
.
【解析】
试题分析:(1)先将 代入函数
代入函数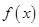 的解析式,并求出导数
的解析式,并求出导数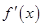 ,然后分别求出
,然后分别求出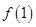 与
与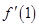 的值,最后利用点斜式求出切线方程;(2)将“函数
的值,最后利用点斜式求出切线方程;(2)将“函数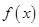 在
在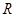 上是增函数”这一条件转化为“不等式
上是增函数”这一条件转化为“不等式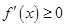 在
在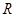 上恒成立”进行求解,结合参数分离法转化为“不等式
上恒成立”进行求解,结合参数分离法转化为“不等式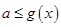 在
在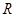 上恒成立”型不等式进行处理,即等价于“
上恒成立”型不等式进行处理,即等价于“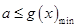 ”,最后利用导数求出函数
”,最后利用导数求出函数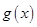 在
在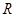 上的最小值,从而得到参数
上的最小值,从而得到参数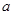 的取值范围.
的取值范围.
试题解析:(1)当 时,
时,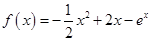 ,则
,则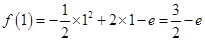 ,
,
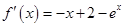 ,
,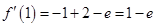 ,
,
故曲线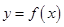 在
在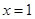 处的切线方程为
处的切线方程为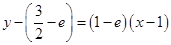 ,即
,即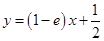 ;
;
(2)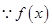 在
在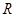 上是增函数,则
上是增函数,则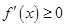 上恒成立,
上恒成立,
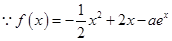 ,
,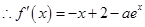 ,
,
于是有不等式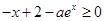 在
在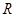 上恒成立,即
上恒成立,即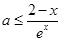 在
在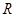 上恒成立,
上恒成立,
令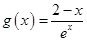 ,则
,则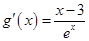 ,令
,令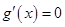 ,解得
,解得 ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
减 |
极小值 |
增 |
故函数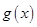 在
在 处取得极小值,亦即最小值,即
处取得极小值,亦即最小值,即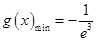 ,所以
,所以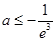 ,
,
即实数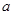 的取值范围是
的取值范围是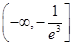 .
.
考点:1.利用导数求切线方程;2.函数不等式恒成立;3.参数分离法

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目









 ,
,
 ,求
,求 的单调区间;
的单调区间; 时,求证:
时,求证: .
.
 .
. 为
为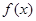 的极值点,求实数
的极值点,求实数 的值;
的值; 在
在 上为增函数,求实数
上为增函数,求实数 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值.
的最大值. 。
。 ,求函数
,求函数 的值;
的值; .
.
 中任取一个元素
中任取一个元素 ,从集合
,从集合 中任取一个元素
中任取一个元素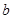 ,求方程
,求方程 有两个不相等实根的概率;
有两个不相等实根的概率; 中任取的一个数,
中任取的一个数, 中任取的一个数,求方程
中任取的一个数,求方程