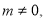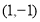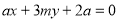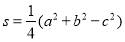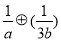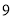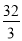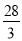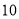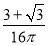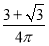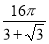题目内容
已知椭圆C的中心在原点,焦点y在轴上,焦距为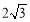 ,且过点M
,且过点M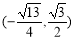 。
。
(1)求椭圆C的方程;
(2)若过点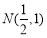 的直线l交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由。
的直线l交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由。
(1)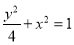 (2)存在,
(2)存在,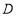
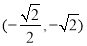
【解析】
试题分析:(1)用椭圆的定义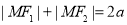 可求
可求 ,根据焦距
,根据焦距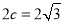 和
和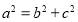 可求
可求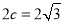 ;也可将点代入设出的椭圆方程解方程组求
;也可将点代入设出的椭圆方程解方程组求 。(2)用点差法求直线
。(2)用点差法求直线 的斜率,设与直线
的斜率,设与直线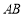 平行且与椭圆相切的直线方程为
平行且与椭圆相切的直线方程为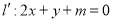 ,直线
,直线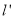 与椭圆的焦点即为所求点
与椭圆的焦点即为所求点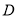 。
。
试题解析:(1)(方法一)依题意,设椭圆方程为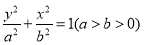 , 1分
, 1分
则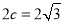 ,
,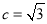 2分
2分
因为椭圆两个焦点为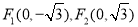 ,所以
,所以
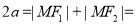
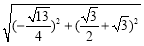
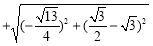 =4 4分
=4 4分
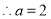
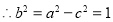 5分
5分
 椭圆
椭圆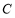 的方程为
的方程为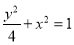 6分
6分
(方法二)依题意,设椭圆方程为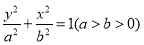 , 1分
, 1分
则 ,即
,即 ,解之得
,解之得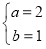 5分
5分
 椭圆C的方程为
椭圆C的方程为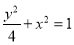 6分
6分
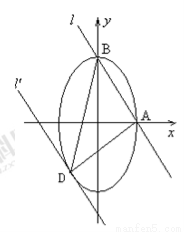
(2)如图
(方法一)设 两点的坐标分别为
两点的坐标分别为 ,
,
则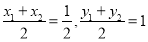 7分
7分
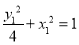 ①
① 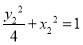 ②
②
①-②,得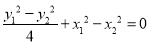 ,
,
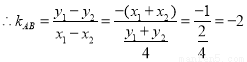 9分
9分
设与直线 平行且与椭圆相切的直线方程为
平行且与椭圆相切的直线方程为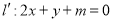
联立方程组 ,消去
,消去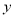 整理得
整理得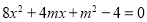
由判别式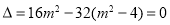 得
得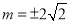 12分
12分
由图知,当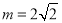 时,
时,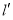 与椭圆的切点为
与椭圆的切点为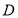 ,此时
,此时
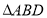 的面积最大
的面积最大
所以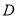 点的坐标为
点的坐标为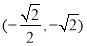 14分
14分
(方法二)设直线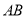 的方程为
的方程为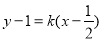 ,联立方程组
,联立方程组 ,
,
消去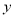 整理得
整理得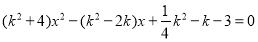
设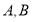 两点的坐标分别为
两点的坐标分别为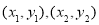 ,则
,则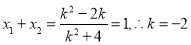
所以直线AB的方程为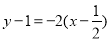 ,即
,即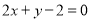 9分(以下同法一)
9分(以下同法一)
考点:1椭圆方程;2点差法解决中点弦问题;3数形结合。

练习册系列答案
相关题目