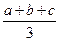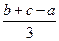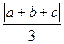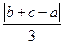题目内容
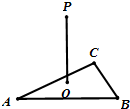
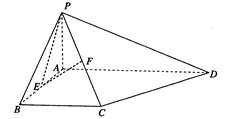
Rt△ABC两直角边分别为3、4，PO⊥面ABC，O是△ABC的内心，PO=
，则点P到△ABC的斜边AB的距离是（ ）
| 3 |
A．
| B．
| C．
| D．2 |
Rt△ABC中，∵AC=4，BC=3，
∴AB=5，
过O作OE⊥AB，垂足是E，作OF⊥BC，垂足是F，作OD⊥AC，交AC于D，
∵O是△ABC的内心，
∴OE=OF=OD=r，（r是△ABC内切圆半径），
∴DC=CF=r，AD=AE=4-r，BF=BE=3-r，
∴AB=3-r+4-r=5，解得r=1，
∴OE=1，
∵PO⊥面ABC，O是△ABC的内心，PO=
，OE⊥AB，
∴PE⊥AB，
PE=
=
=2．
∴点P到△ABC的斜边AB的距离是2．
故选D．
∴AB=5，
过O作OE⊥AB，垂足是E，作OF⊥BC，垂足是F，作OD⊥AC，交AC于D，
∵O是△ABC的内心，
∴OE=OF=OD=r，（r是△ABC内切圆半径），
∴DC=CF=r，AD=AE=4-r，BF=BE=3-r，
∴AB=3-r+4-r=5，解得r=1，
∴OE=1，
∵PO⊥面ABC，O是△ABC的内心，PO=
| 3 |
∴PE⊥AB，
PE=
| PO2+OE2 |
| 3+1 |
∴点P到△ABC的斜边AB的距离是2．
故选D．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
是
的直径，
垂直于
是圆周上不同于
，
的任意一点．
平面
．
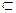α, 则n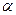
的距离依次为a、b、c，且点A与边BC在平面
