题目内容
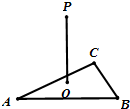
如图所示,A∉平面α,AB、AC是平面α的两条斜线,O是A在平面α内的射影,AO=4,OC=
,BO⊥OC,∠OBA=30°,则C到AB的距离为______.

| 3 |

在Rt△AOB中,
∵AO=4,∠OBA=30°,
∴AB=8,OB=4
∵BO⊥OC,
在Rt△BOC中,由OC=
,
∴BC=
在Rt△AOC中,AC=
在△ABC中,cosB=
=
∴sinB=
则C到AB的距离为BC•sinB=
•
=
故答案为:
∵AO=4,∠OBA=30°,
∴AB=8,OB=4
| 3 |
∵BO⊥OC,
在Rt△BOC中,由OC=
| 3 |
∴BC=
| 51 |
在Rt△AOC中,AC=
| 19 |
在△ABC中,cosB=
|
2
| ||
| 17 |
∴sinB=
| ||
| 17 |
则C到AB的距离为BC•sinB=
| 51 |
| ||
| 17 |
| 15 |
故答案为:
| 15 |

练习册系列答案
相关题目