题目内容
17．已知数列{an}的前n项和为Sn，且an=n•2n，则Sn=（n-1）•2n+1+2．分析 利用“错位相减法”与等比数列的前n项和公式即可得出．
解答 解：∵an=n•2n，
∴Sn=2+2×22+3×23+…+n•2n，
2Sn=22+2×23+…+（n-1）•2n+n•2n+1，
∴-Sn=2+22+…+2n-n•2n+1=$\frac{2（{2}^{n}-1）}{2-1}$-n•2n+1=（1-n）•2n+1-2，
∴Sn=（n-1）•2n+1+2，
故答案为：（n-1）•2n+1+2．
点评 本题考查了“错位相减法”与等比数列的前n项和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
5．已知向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（2，m2），若$\overrightarrow{a}$∥$\overrightarrow{b}$，则 m的值为（ ）
| A． | 2或-1 | B． | -2或1 | C． | ±2 | D． | ±1 |
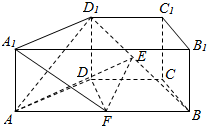如图，直四棱柱ABCD-A1B1C1D1中，底面ABCD是等腰梯形，AB∥CD，AB=2DC=2，E为BD1的中点，F为AB的中点，∠DAB=60°．
6．f（x）为奇函数，且在（-∞，0）为递增，f（-2）=0，则xf（x）＞0的解集为（ ）
| A． | （-∞，-2）∪（2，+∞） | B． | （-∞，-2）∪（0，2） | C． | （-2，0）∪（0，2） | D． | （-2，0）∪（2，+∞） |