Question

(本题满分10分)

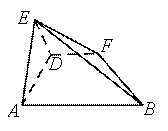
（第20题）

如图，平面平面，为正三角形，四边形为直角梯形，且∠BAD = 90°，AB∥DF，，AB =a, DF = 。

   （I）求证：；

（II）求二面角的大小;

   （Ⅲ）点P是线段EB上的动点，当为直角时，求BP 的长度.

Answer 1

(本题满分10分)

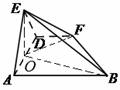
（第20题）

（I）连结，则

，

，，

所以，即.

又因为，所以平面，得.                   3分

方法一

（Ⅱ） 平面平面，过点向引垂线交于点，连结，延长DF到点C，使CD = AB，

则，

，

，

所以，即为二面角的平面角，

在中，，所以．                        6分

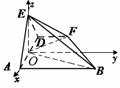
（第20题）

方法二：（II ）取AD的中点O，连结OE，则EOAD，EO平面ABCDD，建立如图所示的直角坐标系，设，则，则，

则，

所以,，

可求得平面的法向量为，平面的一个法向量为，

则二面角的大小为，，即二面角为．          6分

（Ⅲ）设，（）则

 

，     同理，，   8分

，

  由=0，解得t=或，

所以BP = .                                                10分