Question

（本题满分12分）

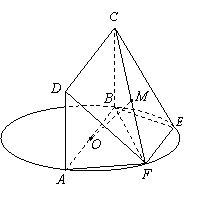
如图，三棱锥P-ABC中，PA⊥底面ABC，AB⊥BC，DE垂直平分线段PC，且分别交AC、PC于D、E两点,又PB=BC，PA=AB。

（1）求证：PC⊥平面BDE；

（2）若点Q是线段PA上任一点，判断BD、DQ的位置关系，

并证明你的结论；

（3）若AB=2,求三棱锥B-CED的体积

Answer 1

（1）证明：由等腰三角形PBC，得BE⊥PC    又DE垂直平分PC，∴DE⊥PC 

 ∴PC⊥平面BDE………… 4分

（2）由（Ⅰ），有PC⊥BD     因为 PA⊥底面ABC ，所以PA⊥BD      ……………6分

     

  所以点Q是线段PA上任一点都有BD⊥DQ       

（3）解：  

                              

且 ， ∽

      

 由（2）知：

………12分