题目内容
如图，某几何体的正视图和俯视图都是矩形，侧视图是平行四边形，则该几何体的表面积为（ ）
A、15+3
| ||
B、9
| ||
C、30+6
| ||
D、18
|
分析：由已知中三视图可以确定，该几何体是以侧视图为底面的直四棱柱，根据已知三视图中标识的数据，求出棱柱的底面积和侧面积，即可得到答案．
解答：解：由已知中三视图该几何体为四棱柱，
其底面底边长为2+
=3，侧视图的高为：
，
故底面积S=2×3
=6
，
又因为棱柱的高为3，
故侧面积为：（2+3+2+3）×3=30．
∴几何体的表面积为：30+6
．
故选：C．
其底面底边长为2+
22-(
|
| 3 |
故底面积S=2×3
| 3 |
| 3 |
又因为棱柱的高为3，
故侧面积为：（2+3+2+3）×3=30．
∴几何体的表面积为：30+6
| 3 |
故选：C．
点评：本题考查的知识点是由三视图求表面积，其中根据三视图判断出几何体的形状及相应底面面积和高是解答本题的关键．
练习册系列答案
相关题目
（2012•江门一模）如图，某几何体的正视图和侧视图都是对角线长分别为4和3的菱形，俯视图是对角线长为3的正方形，则该几何体的体积为（ ）
（2014•郑州一模）如图，某几何体的正视图和俯视图都是矩形，侧视图是平行四边形，则该几何体的体积为（ ）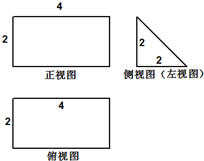
（2012•珠海一模）如图，某几何体的正视图和俯视图都是矩形，侧视图是等腰直角三角形，则该几何体的体积为（ ）
B．
C．
D．