题目内容
已知函数f(x)=x2-2ax+a在区间(1,3)内有极小值,则函数g(x)= 在区间(1,+∝)上一定
在区间(1,+∝)上一定
- A.有最小值
- B.有最大值
- C.是减函数
- D.是增函数
A
分析:根据函数在区间(1,3)内有极小值先确定a的取值范围,再化简函数g(x)由基本不等式可得答案.
解答:∵函数f(x)=x2-2ax+a在区间(1,3)内有极小值,
∴f′(x)=2x-2a=0在(1,3)有解
∴1<a<3.g(x)=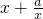 -2a在区间(0,
-2a在区间(0, )内单调递减,在区间(
)内单调递减,在区间( )内单调递增.
)内单调递增.
∵ >1,
>1,
∴函数g(x)在区间(1,+∝)上一定有最小值.
故选A.
点评:本题主要考查函数求导和基本不等式的有关问题.注意极小值一定是党导数等于0时取到.
分析:根据函数在区间(1,3)内有极小值先确定a的取值范围,再化简函数g(x)由基本不等式可得答案.
解答:∵函数f(x)=x2-2ax+a在区间(1,3)内有极小值,
∴f′(x)=2x-2a=0在(1,3)有解
∴1<a<3.g(x)=
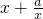 -2a在区间(0,
-2a在区间(0, )内单调递减,在区间(
)内单调递减,在区间( )内单调递增.
)内单调递增.∵
 >1,
>1,∴函数g(x)在区间(1,+∝)上一定有最小值.
故选A.
点评:本题主要考查函数求导和基本不等式的有关问题.注意极小值一定是党导数等于0时取到.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|