题目内容
已知m为实常数,设命题p:函数 在其定义域内为减函数;命题q:x1和x2是方程x2-ax-2=0的两个实根,不等式|m2-5m-3|≥|x1-x2|对任意实数a∈[-1,1]恒成立.
在其定义域内为减函数;命题q:x1和x2是方程x2-ax-2=0的两个实根,不等式|m2-5m-3|≥|x1-x2|对任意实数a∈[-1,1]恒成立.(1)当p是真命题,求m的取值范围;
(2)当“p或q”为真命题,“p且q”为假命题时,求m的取值范围.
【答案】分析:(1)由题条件,先利用导数知识求解p为真时m的范围
(2)由p或q”为真命题,“p且q”为假命题可知P,q中一个为真,一个为假,分类讨论即可求解
解答:解:(1)∵ 的定义域内为R
的定义域内为R
∵ =
= ll=
ll=
∵函数 在其定义域内为减函数
在其定义域内为减函数
∴f′(x)= ≤0恒成立
≤0恒成立
∴
∴m≥1
(Ⅱ)由x1和x2是方程x2-ax-2=0的两个实根可得,x1+x2=a,x1x2=-2
∴ =
=
当a∈[-1,1]时,a2+8≤9即|x1-x2|≤3 …(7分)
由题意不等式|m2-5m-3|≥|x1-x2|对任意实数a∈[-1,1]恒成立的解集等价于|m2-5m-3|≥3的解集
∴m2-5m-3≥-3(1)或m2-5m-3≤-3(2)
由(1)可得m≤-1或m≥6
由(2)可得0≤m≤5
所以,当m≤-1或0≤m≤5或m≥6时,q是真命题.…(9分)
又由题意可知p、q为一真一假.
当p真q假时,解得5<m<6;当p假q真时,解得m≤-1或0≤m<1 …(10分)
综上所述,所求m的取值范围为(-∞,-1]∪[0,1]∪(5,6)…(13分)
点评:本题必要条件、充分条件与充要条件的判断与应用,求解本题关键是对p条件中恒成立问题的正确转化以及q条件中只有一个实数满足不等式这个存在性问题的正确理解与转化.此两点也是本题的易错点.
(2)由p或q”为真命题,“p且q”为假命题可知P,q中一个为真,一个为假,分类讨论即可求解
解答:解:(1)∵
 的定义域内为R
的定义域内为R∵
 =
= ll=
ll=
∵函数
 在其定义域内为减函数
在其定义域内为减函数∴f′(x)=
 ≤0恒成立
≤0恒成立∴

∴m≥1
(Ⅱ)由x1和x2是方程x2-ax-2=0的两个实根可得,x1+x2=a,x1x2=-2
∴
 =
=
当a∈[-1,1]时,a2+8≤9即|x1-x2|≤3 …(7分)
由题意不等式|m2-5m-3|≥|x1-x2|对任意实数a∈[-1,1]恒成立的解集等价于|m2-5m-3|≥3的解集
∴m2-5m-3≥-3(1)或m2-5m-3≤-3(2)
由(1)可得m≤-1或m≥6
由(2)可得0≤m≤5
所以,当m≤-1或0≤m≤5或m≥6时,q是真命题.…(9分)
又由题意可知p、q为一真一假.
当p真q假时,解得5<m<6;当p假q真时,解得m≤-1或0≤m<1 …(10分)
综上所述,所求m的取值范围为(-∞,-1]∪[0,1]∪(5,6)…(13分)
点评:本题必要条件、充分条件与充要条件的判断与应用,求解本题关键是对p条件中恒成立问题的正确转化以及q条件中只有一个实数满足不等式这个存在性问题的正确理解与转化.此两点也是本题的易错点.

练习册系列答案
相关题目
 在其定义域内为减函数;命题
在其定义域内为减函数;命题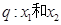 是方程
是方程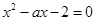 的两上实根,不等式
的两上实根,不等式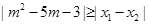 对任意实数
对任意实数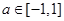 恒成立。
恒成立。