题目内容
已知函数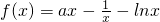 ,a∈R,
,a∈R,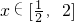 .
.
(1)当a=-2时,求f(x)的最大值;
(2)设g(x)=[f(x)+lnx]•x2,k是g(x)图象上不同的两点的连线的斜率,是否存在实数a,使得k<1恒成立?若存在,求a的取值范围;若不存在,请说明理由.
解:f(x)的定义域为 ,
,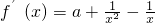
(1)当a=-2时,在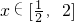 ,
,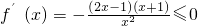 ,
,
所以f(x)在区间 上单调递减,
上单调递减,
故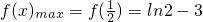 .
.
(2)存在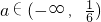 符合条件.
符合条件.
解法一:据题意在y=g(x)=[f(x)+lnx]•x2=ax3-x图象上总可以找到一点P0(x0,y0)使以p为切点的切线平行图象上的任意两点的连线,
即存在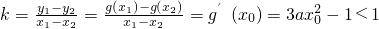 恒成立,
恒成立,
因为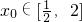 ,所以
,所以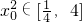 ,所以
,所以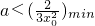 =
=
故存在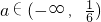 符合条件.
符合条件.
解法二:g(x)=[f(x)+lnx]•x2=ax3-x,不妨设任意不同两点P1(x1,y1),P2(x2,y2)其中x1<x2,则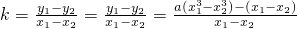 =
=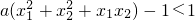
由于k<1恒成立,则k<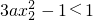 恒成立,知
恒成立,知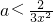 恒成立…(12分)
恒成立…(12分)
因为 ,所以
,所以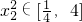 ,故
,故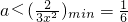 ,分)
,分)
故存在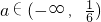 符合条件.
符合条件.
(1)当a=-2时,求导函数,确定f(x)在区间 上单调递减,从而可求f(x)的最大值;
上单调递减,从而可求f(x)的最大值;
(2)存在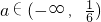 符合条件.
符合条件.
解法一:据题意存在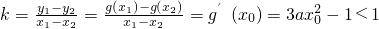 ,分离参数,可得结论;
,分离参数,可得结论;
解法二:据题意存在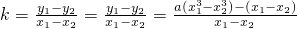 =
=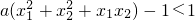 ,分离参数,可得结论.
,分离参数,可得结论.
点评:本题考查导数知识的运用,考查函数的最值,考查导数的几何意义,考查恒成立问题,考查分离参数法的运用,属于中档题.
 ,
,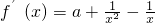
(1)当a=-2时,在
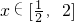 ,
,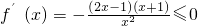 ,
,所以f(x)在区间
 上单调递减,
上单调递减,故
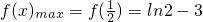 .
.(2)存在
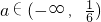 符合条件.
符合条件.解法一:据题意在y=g(x)=[f(x)+lnx]•x2=ax3-x图象上总可以找到一点P0(x0,y0)使以p为切点的切线平行图象上的任意两点的连线,
即存在
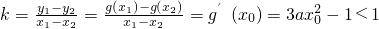 恒成立,
恒成立,因为
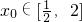 ,所以
,所以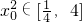 ,所以
,所以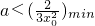 =
=
故存在
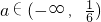 符合条件.
符合条件. 解法二:g(x)=[f(x)+lnx]•x2=ax3-x,不妨设任意不同两点P1(x1,y1),P2(x2,y2)其中x1<x2,则
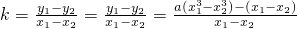 =
=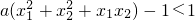
由于k<1恒成立,则k<
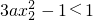 恒成立,知
恒成立,知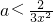 恒成立…(12分)
恒成立…(12分)因为
 ,所以
,所以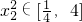 ,故
,故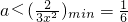 ,分)
,分)故存在
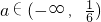 符合条件.
符合条件.(1)当a=-2时,求导函数,确定f(x)在区间
 上单调递减,从而可求f(x)的最大值;
上单调递减,从而可求f(x)的最大值;(2)存在
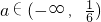 符合条件.
符合条件.解法一:据题意存在
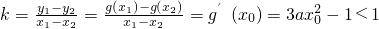 ,分离参数,可得结论;
,分离参数,可得结论;解法二:据题意存在
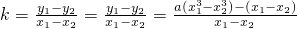 =
=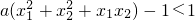 ,分离参数,可得结论.
,分离参数,可得结论.点评:本题考查导数知识的运用,考查函数的最值,考查导数的几何意义,考查恒成立问题,考查分离参数法的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (a∈R且a≠0).
(a∈R且a≠0).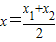 ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. ,a∈R.
,a∈R. 上的任意一个x,都有f(x)≤1成立,求a的取值范围.
上的任意一个x,都有f(x)≤1成立,求a的取值范围. (a∈R).
(a∈R). 在[1,e]上是增函数,求a的取值范围;
在[1,e]上是增函数,求a的取值范围;
 .
.