题目内容
如图,已知平面A1B1C1平行于三棱锥V-ABC的底面ABC,等边△AB1C所在的平面与底面ABC垂直,且∠ACB=90°,设AC=2a,BC=a,
(1)求证直线B1C1是异面直线AB1与A1C1的公垂线;
(2)求点A到平面VBC的距离;
(3)求二面角A-VB-C的大小。
(1)求证直线B1C1是异面直线AB1与A1C1的公垂线;
(2)求点A到平面VBC的距离;
(3)求二面角A-VB-C的大小。
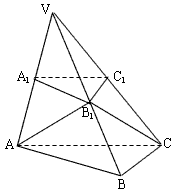
解:(1)∵平面 ∥平面ABC, ∥平面ABC,∴  , , , ,∴  , ,又∵平面  ⊥平面ABC,平面 ⊥平面ABC,平面 ∩平面ABC=AC, ∩平面ABC=AC,∴BC⊥平面  , ,∴  ,∴ ,∴ , ,又  , , , ,∴B1C1为AB1与A1C1的公垂线。 |
|
|
(2)过A作 |
 |

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 于D,
于D, 为正三角形,
为正三角形, ,∴BC⊥AD,
,∴BC⊥AD, ,
, 中,
中, ,
, 。
。  中,
中, ,
, ,
, ,
, ,∴
,∴ ,
, 。
。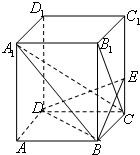 如图,已知正四棱柱ABCD-A1B1C1D1中,2AB=BB1,
如图,已知正四棱柱ABCD-A1B1C1D1中,2AB=BB1,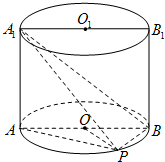 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为20π,OA=2,∠AOP=120°.
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为20π,OA=2,∠AOP=120°.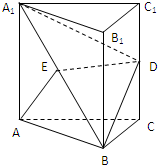 如图,已知正三棱柱ABC-A1B1C1,AA1=AB=2a,D、E分别为CC1、A1B的中点.
如图,已知正三棱柱ABC-A1B1C1,AA1=AB=2a,D、E分别为CC1、A1B的中点. 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F. 如图,已知棱长为1的正方体ABCD-A1B1C1D1.
如图,已知棱长为1的正方体ABCD-A1B1C1D1.