题目内容
已知 为等比数列,
为等比数列, 是等差数列,
是等差数列,
(Ⅰ)求数列 的通项公式及前
的通项公式及前 项和
项和 ;
;
(2)设
 ,
,
 ,其中
,其中 ,试比较
,试比较 与
与 的大小,并加以证明.
的大小,并加以证明.
【答案】
(Ⅰ)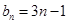 ,
,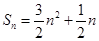 ;(Ⅱ)当
;(Ⅱ)当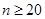 时,
时,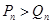 ;当
;当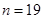 时,
时,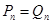 ;当
;当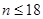 时,
时,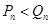 .
.
【解析】
试题分析:(Ⅰ)求数列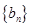 的通项公式及前
的通项公式及前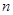 项和
项和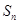 ,由已知
,由已知 是等差数列,且
是等差数列,且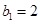 ,只需求出公差
,只需求出公差 即可,由已知
即可,由已知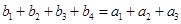 ,且
,且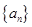 为等比数列,
为等比数列,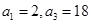 ,只需求出公比
,只需求出公比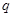 即可,由
即可,由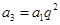 得,
得,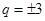 ,讨论是否符合条件
,讨论是否符合条件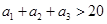 ,从而得
,从而得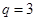 ,这样问就可以解决;(Ⅱ)设
,这样问就可以解决;(Ⅱ)设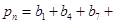
 ,
,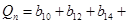
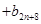 ,其中
,其中 ,试比较
,试比较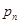 与
与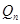 的大小,关键是求出
的大小,关键是求出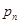 与
与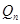 的关系式,由已知
的关系式,由已知 是等差数列,由(Ⅰ)知
是等差数列,由(Ⅰ)知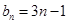 ,即可写出
,即可写出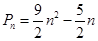 ,
,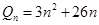 ,两式作差得
,两式作差得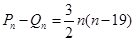 ,讨论即可.
,讨论即可.
试题解析:(Ⅰ)设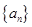 的公比为
的公比为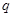 ,由
,由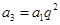 得,
得,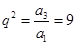 ,
,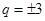 。 1分
。 1分
当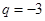 时,
时,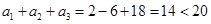 ,这与
,这与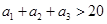 矛盾 2分
矛盾 2分
当 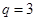 时,
时,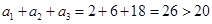 ,符合题意。 3分
,符合题意。 3分
设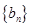 的公差为
的公差为 ,由
,由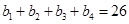 ,得:
,得: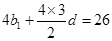
又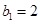
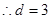
 5分
5分
所以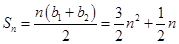 7分
7分
(Ⅱ)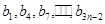 组成公差为
组成公差为 的等差数列,所以
的等差数列,所以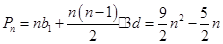 8分
8分
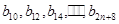 组成公差为
组成公差为 的等差数列, 所以
的等差数列, 所以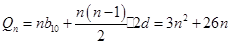
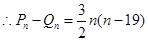 10分
10分
故当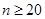 时,
时,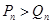 ;当
;当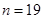 时,
时,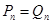 ;当
;当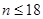 时,
时,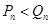 12分
12分
考点:等比数列,等差数列的通项公式,等差数列的前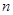 项和
项和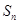 ,比较大小.
,比较大小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为等比数列,
为等比数列, 是它的前
是它的前 项和,若
项和,若 ,
, 、
、 的等比中项为
的等比中项为 ,则
,则 =(
)
=(
) B.63
C.
B.63
C. D.127
D.127