题目内容
箱中装有4个白球和m(m∈N*)个黑球.规定取出一个白球得2分,取出一个黑球得1分,现从箱中任取3个球,假设每个球被取出的可能性都相等.记随机变量X为取出的3个球所得分数之和.
(I)若P(X=6)=
,求m的值;
(II)当m=3时,求X的分布列和数字期望E(X).
(I)若P(X=6)=
| 2 | 5 |
(II)当m=3时,求X的分布列和数字期望E(X).
分析:(I)取出的3个球都是白球时,随机变量X=6,利用概率公式,建立方程,即可求m的值;
(II)当m=3时,确定X的取值,求出相应的概率,即可求X的分布列和数字期望E(X).
(II)当m=3时,确定X的取值,求出相应的概率,即可求X的分布列和数字期望E(X).
解答:解:(I)由题意得取出的3个球都是白球时,随机变量X=6.(1分)
所以P(X=6)=
=
,(3分)
即
=10,
解得m=1.(5分)
(II)由题意得X的可能取值为3,4,5,6.(6分)
则P(X=3)=
=
,P(X=4)=
=
,
P(X=5)=
=
.P(X=6)=
=
.(10分)
X的分布列为:
(11分)
所以E(X)=3×
+4×
+5×
+6×
=
.(13分)
所以P(X=6)=
| ||
|
| 2 |
| 5 |
即
| C | 3 m+4 |
解得m=1.(5分)
(II)由题意得X的可能取值为3,4,5,6.(6分)
则P(X=3)=
| ||
|
| 1 |
| 35 |
| ||||
|
| 12 |
| 35 |
P(X=5)=
| ||||
|
| 18 |
| 35 |
| ||
|
| 4 |
| 35 |
X的分布列为:
| X | 3 | 4 | 5 | 6 | ||||||||
| P |
|
|
|
|
所以E(X)=3×
| 1 |
| 35 |
| 12 |
| 35 |
| 18 |
| 35 |
| 4 |
| 35 |
| 33 |
| 7 |
点评:本题考查概率的计算,考查离散型随机变量的分布列与期望,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
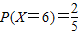 ,求m的值;
,求m的值;