题目内容
已知函数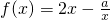 的定义域为(0,1](a为实数).
的定义域为(0,1](a为实数).
(1)当a=-1时,求函数y=f(x)的值域;
(2)当a>0时,判断函数y=f(x)的单调性并给予证明;
(3)若f(x)>5在定义域上恒成立,求实数a的取值范围.
解:(1)显然函数y=f(x)的值域为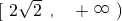 .
.
(2)当a>0时,y=f(x)在(0,1]上为单调递增函数.证明如下:任取x1,x2∈(0,1],且x1<x2,
则f(x1)-f(x2)=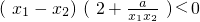 ,所以y=f(x)在(0,1]上为单调递增函数.
,所以y=f(x)在(0,1]上为单调递增函数.
(3)当x∈(0,1]时,f(x)>5在定义域上恒成立,即a<2x2-5x在x∈(0,1]时恒成立.
设g(x)=2x2-5x,当x∈(0,1]时,g(x)∈[-3,0),只要a<-3即可,即a的取值范围是(-∞,-3).
分析:(1)将a的值代入函数解析式,利用基本不等式求出函数的值域.
(2)当a>0时,y=f(x)在(0,1]上为单调递增函数,再利用定义证明;
(3)当x∈(0,1]时,f(x)>5在定义域上恒成立,等价于a<2x2-5x在x∈(0,1]时恒成立,求函数.g(x)=2x2-5x的最小值即可.
点评:本题主要考查函数的值域,考查函数的单调性及恒成立问题,有一定的综合性.
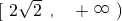 .
.(2)当a>0时,y=f(x)在(0,1]上为单调递增函数.证明如下:任取x1,x2∈(0,1],且x1<x2,
则f(x1)-f(x2)=
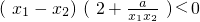 ,所以y=f(x)在(0,1]上为单调递增函数.
,所以y=f(x)在(0,1]上为单调递增函数.(3)当x∈(0,1]时,f(x)>5在定义域上恒成立,即a<2x2-5x在x∈(0,1]时恒成立.
设g(x)=2x2-5x,当x∈(0,1]时,g(x)∈[-3,0),只要a<-3即可,即a的取值范围是(-∞,-3).
分析:(1)将a的值代入函数解析式,利用基本不等式求出函数的值域.
(2)当a>0时,y=f(x)在(0,1]上为单调递增函数,再利用定义证明;
(3)当x∈(0,1]时,f(x)>5在定义域上恒成立,等价于a<2x2-5x在x∈(0,1]时恒成立,求函数.g(x)=2x2-5x的最小值即可.
点评:本题主要考查函数的值域,考查函数的单调性及恒成立问题,有一定的综合性.

练习册系列答案
相关题目
已知函数 的定义域为
的定义域为 ,部分对应值如下表。
,部分对应值如下表。 的导函数
的导函数 的图像如图所示。
的图像如图所示。
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|

下列关于函数 的命题:
的命题:
①函数 在
在 上是减函数;②如果当
上是减函数;②如果当 时,
时, 最大值是
最大值是 ,那么
,那么 的最大值为
的最大值为 ;③函数
;③函数 有
有 个零点,则
个零点,则 ;④已知
;④已知 是
是 的一个单调递减区间,则
的一个单调递减区间,则 的最大值为
的最大值为 。
。
其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
 的定义域为
的定义域为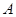 ,
,  ,且
,且 的真子集,求实数
的真子集,求实数 的取值范围.
的取值范围.




 的定义域为
的定义域为 ,且
,且 ,
, 为
为 ,
, 满足
满足 ,则
,则 的取值范围是
的取值范围是
 B.
B. C.
C. D.
D.