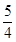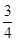题目内容
若函数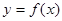 是定义在区间
是定义在区间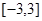 上的奇函数,且在
上的奇函数,且在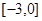 上单调递增,若
上单调递增,若
实数 满足:
满足: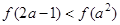 ,求
,求 的取值范围.
的取值范围.
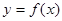 是定义在区间
是定义在区间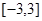 上的奇函数,且在
上的奇函数,且在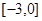 上单调递增,若
上单调递增,若实数
 满足:
满足: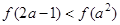 ,求
,求 的取值范围.
的取值范围. 
由于f(x) 是定义在区间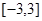 上的奇函数,且在
上的奇函数,且在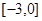 上单调递增,所以函
上单调递增,所以函
数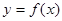 是定义域上的增函数.从而把不等式
是定义域上的增函数.从而把不等式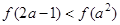 转化为不等式组
转化为不等式组
 来求解.
来求解.
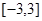 上的奇函数,且在
上的奇函数,且在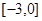 上单调递增,所以函
上单调递增,所以函数
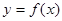 是定义域上的增函数.从而把不等式
是定义域上的增函数.从而把不等式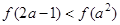 转化为不等式组
转化为不等式组 来求解.
来求解.
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
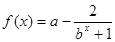
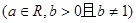
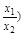 +f(x2)=f(x1),且当x>1时,f(x)<0.
+f(x2)=f(x1),且当x>1时,f(x)<0. 是奇函数,(a,b,c∈Z),且f(1)=2,f(2)<3,求a,b,c的值。
是奇函数,(a,b,c∈Z),且f(1)=2,f(2)<3,求a,b,c的值。 时,不等式
时,不等式 恒成立,则
恒成立,则 的取值范围是 .
的取值范围是 . 的最大值为( )
的最大值为( )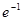
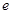
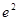
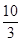
 ,
,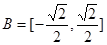 ,函数
,函数 ,
,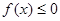 的解集为C,当
的解集为C,当 时,求实数
时,求实数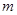 取值范围;
取值范围; ,都有
,都有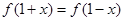 成立,试求
成立,试求 时,
时,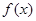 的值域;
的值域;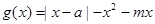
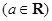 ,求
,求 的最小值.
的最小值.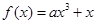 恰有3个单调区间,则a的取值范围为
恰有3个单调区间,则a的取值范围为  的最大值是( )
的最大值是( )