题目内容
设函数f（x）=x+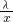
，其中常数λ＞0．
（1）判断函数的奇偶性；
（2）若λ=1，判断f（x）在区间[1，+∞）上的单调性，并用定义加以证明；
（3）若f（x）在区间[1，+∞）上单调递增，求常数λ的取值范围．
解：（1）由于函数f（x）=x+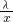，其中常数λ＞0，故函数的定义域为R，
且f（-x）=-x+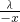
=-f（x），故函数为奇函数．
（2）函数f（x）在区间[1，+∞）上单调递增．
证明：任取1≤x1＜x2，∵f（x1）-f（x2）=（x1+
）-（x2+
）=（x1-x2）+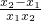
=（x1-x2）•
，
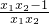由1≤x1＜x2，可得 x1-x2 ＜0，x1•x2，＞1，∴f（x1）＜f（x2），
故函数f（x）在区间[1，+∞）上单调递增．…
（3）任取1≤x1＜x2，∵f（x1）-f（x2）=（x1+
）-（x2+
）=）=（x1-x2）+λ•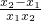=（x1-x2）•
，
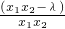且函数f（x）在区间[1，+∞）上的单调递增．∴f（x1）-f（x2）＜0，
∴x1•x2-λ＞0 对1≤x1＜x2 恒成立，∴λ＜x1•x2，再由1＜x1•x2，可得0＜λ≤1．…
分析：（1）函数的定义域为R，且f（-x）=-x+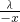=-f（x），可得函数为奇函数．
（2）任取1≤x1＜x2，计算f（x1）-f（x2）=（x1-x2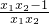）•＜0，可得 f（x1）＜f（x2），从而得到函数f（x）在区间[1，+∞）上单调递增．
（3）任取1≤x1＜x2，根据f（x1）-f（x2）=（x1-x2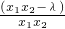）•，且函数f（x）在区间[1，+∞）上的单调递增，可得f（x1）-f（x2）＜0，
即 λ＜x1•x2 对1≤x1＜x2 恒成立．再由1＜x1•x2，可得λ的范围．
点评：本题主要考查函数的奇偶性的判断，函数的单调性的判断和证明，属于中档题．
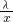，其中常数λ＞0，故函数的定义域为R，且f（-x）=-x+
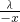=-f（x），故函数为奇函数． （2）函数f（x）在区间[1，+∞）上单调递增．
证明：任取1≤x1＜x2，∵f（x1）-f（x2）=（x1+
）-（x2+）=（x1-x2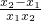）+=（x1-x2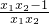）•，由1≤x1＜x2，可得 x1-x2 ＜0，x1•x2，＞1，∴f（x1）＜f（x2），
故函数f（x）在区间[1，+∞）上单调递增．…
（3）任取1≤x1＜x2，∵f（x1）-f（x2）=（x1+
）-（x2+）=）=（x1-x2）+λ•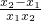=（x1-x2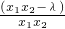）•，且函数f（x）在区间[1，+∞）上的单调递增．∴f（x1）-f（x2）＜0，
∴x1•x2-λ＞0 对1≤x1＜x2 恒成立，∴λ＜x1•x2，再由1＜x1•x2，可得0＜λ≤1．…
分析：（1）函数的定义域为R，且f（-x）=-x+
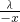=-f（x），可得函数为奇函数． （2）任取1≤x1＜x2，计算f（x1）-f（x2）=（x1-x2）•
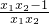＜0，可得 f（x1）＜f（x2），从而得到函数f（x）在区间[1，+∞）上单调递增．（3）任取1≤x1＜x2，根据f（x1）-f（x2）=（x1-x2）•
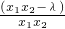，且函数f（x）在区间[1，+∞）上的单调递增，可得f（x1）-f（x2）＜0，即 λ＜x1•x2 对1≤x1＜x2 恒成立．再由1＜x1•x2，可得λ的范围．
点评：本题主要考查函数的奇偶性的判断，函数的单调性的判断和证明，属于中档题．
练习册系列答案
相关题目
设函数f（x）的定义域为A，若存在非零实数t，使得对于任意x∈C（C⊆A），有x+t∈A，且f（x+t）≤f（x），则称f（x）为C上的t低调函数．如果定义域为[0，+∞）的函数f（x）=-|x-m2|+m2，且 f（x）为[0，+∞）上的10低调函数，那么实数m的取值范围是（ ）
| A、[-5，5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|