Question

14．已知函数f（x）=$\left\{\begin{array}{l}{-x，x∈[-1，0）}\\{\frac{1}{f（x-1）}-1，x∈[0，1）}\end{array}\right.$，若方程f（x）-kx-3k=0有两个实数根，则k的取值范围是（0，$\frac{1}{2}$]．

Answer 1

分析 化简f（x）=$\left\{\begin{array}{l}{-x，x∈[-1，0）}\\{\frac{1}{-（x-1）}-1，x∈[0，1）}\end{array}\right.$，作其与y=k（x+3）的图象，从而利用数形结合的方法求解．

解答 解：由题意，f（x）=$\left\{\begin{array}{l}{-x，x∈[-1，0）}\\{\frac{1}{-（x-1）}-1，x∈[0，1）}\end{array}\right.$，
作函数f（x）=$\left\{\begin{array}{l}{-x，x∈[-1，0）}\\{\frac{1}{-（x-1）}-1，x∈[0，1）}\end{array}\right.$与y=k（x+3）的图象如下，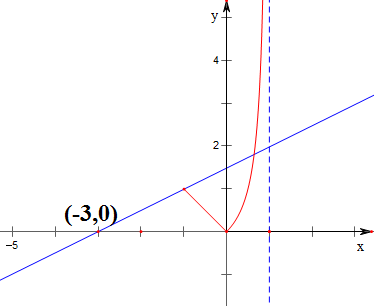

直线y=k（x+3）的图象恒过点（-3，0），
当过点（-1，1）时，直线y=k（x+3）中k=$\frac{1}{2}$，此时为临界值，
故k的取值范围是（0，$\frac{1}{2}$]．
故答案为：（0，$\frac{1}{2}$]．

点评 本题考查了数形结合的思想应用及函数的化简与几何意义的应用．