题目内容
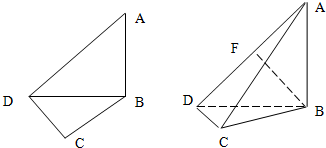
 如图,在平面四边形ABCD中,△BCD是正三角形,AB=AD=1,∠BAD=θ.
如图,在平面四边形ABCD中,△BCD是正三角形,AB=AD=1,∠BAD=θ.(Ⅰ)将四边形ABCD的面积S表示成关于θ的函数;
(Ⅱ)求S的最大值及此时θ的值.
分析:(Ⅰ)在△ABD中,根据余弦定理可表示BD,根据S=
absinc可表示出△ABD,△BCD的面积,从而表示出四边形ABCD的面积;
(Ⅱ)由(Ⅰ)可把四边形面积S化为S=Asin(ωx+φ)+B形式,根据三角函数的有界性可求其最值.
| 1 |
| 2 |
(Ⅱ)由(Ⅰ)可把四边形面积S化为S=Asin(ωx+φ)+B形式,根据三角函数的有界性可求其最值.
解答:解:(Ⅰ)BD=
=
,
S△ABD=
×1×1×sinθ=
sinθ,
S△BCD=
×BD2=
(2-2cosθ)=
-
cosθ,
∴SABCD=
sinθ-
cosθ+
(0<θ<π).
(Ⅱ)由(Ⅰ)得SABCD=
sinθ-
cosθ+
=sin(θ-
)+
,
∵0<θ<π,∴-
<θ-
<
,
当θ-
=
时,即θ=
时,S有最大值1+
.
| 12+12-2×1×1cosθ |
| 2-2cosθ |
S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
S△BCD=
| ||
| 4 |
| ||
| 4 |
| ||
| 2 |
| ||
| 2 |
∴SABCD=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
(Ⅱ)由(Ⅰ)得SABCD=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| π |
| 3 |
| ||
| 2 |
∵0<θ<π,∴-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
当θ-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
| ||
| 2 |
点评:本题考查三角函数最值的求法,考查三角恒等变换知识,考查学生分析解决问题的能力.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图,在平面四边形ABCD中,若AB=2,CD=1,则
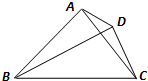
如图,在平面四边形ABCD中,若AB=2,CD=1,则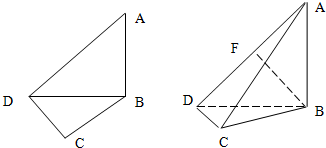 如图,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC,设点F为棱AD的中点.
如图,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC,设点F为棱AD的中点.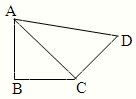 如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.
如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.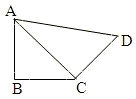 如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.
如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.