题目内容
(本小题满分12分)
海关对同时从 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如右表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如右表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测
| 地区 |  |  |  |
| 数量 | 50 | 150 | 100 |
(1)求这6件样品中来自
 各地区商品的数量;
各地区商品的数量;(2)若在这6件样品中随机抽取2件送往甲机构进一步检测,求这2件商品来自相同地区的概率.
(1) A,B,C三个地区的商品被选取的件数分别为1,3,2.
(2)这2件商品来自相同地区的概率为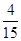 .
.
解析试题分析:(1)首先确定样本容量与总体中的个数的比是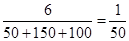 ,
,
从而得到样本中包含三个地区的个体数量分别是: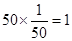 ,
,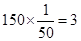 ,
,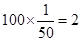 .
.
(2)设6件来自A,B,C三个地区的样品分别为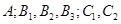 ,
,
写出抽取的这2件商品构成的所有基本事件: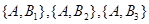 ,
,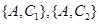 ,
,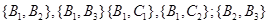 ,
,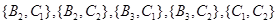 ,共15个.
,共15个.
记事件D:“抽取的这2件商品来自相同地区”,
写出事件D包含的基本事件: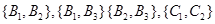 共4个.
共4个.
由每个样品被抽到的机会均等,因此这些基本事件的出现是等可能的,
利用古典概型概率的计算公式得解.
试题解析:(1)因为样本容量与总体中的个数的比是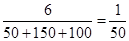 ,
,
所以样本中包含三个地区的个体数量分别是: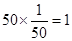 ,
,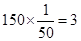 ,
,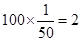 ,
,
所以A,B,C三个地区的商品被选取的件数分别为1,3,2.
(2)设6件来自A,B,C三个地区的样品分别为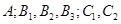 ,
,
则抽取的这2件商品构成的所有基本事件为: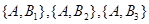 ,
,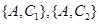 ,
,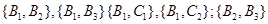 ,
,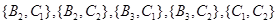 ,共15个.
,共15个.
每个样品被抽到的机会均等,因此这些基本事件的出现是等可能的,
记事件D:“抽取的这2件商品来自相同地区”,
则事件D包含的基本事件有: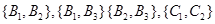 共4个.
共4个.
所有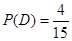 ,即这2件商品来自相同地区的概率为
,即这2件商品来自相同地区的概率为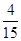 .
.
考点:分层抽样,古典概型.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案某中学对高二甲、乙两个同类班级进行加强语文阅读理解训练对提高数学应用题得分率作用的试验,其中甲班为实验班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用试题测试的平均成绩(均取整数)如表所示:
| | 60分以下 | 61﹣70分 | 71﹣80分 | 81﹣90分 | 91﹣100分 |
| 甲班(人数) | 3 | 6 | 11 | 18 | 12 |
| 乙班(人数) | 3 | 9 | 13 | 15 | 10 |
现规定平均成绩在80分以上(不含80分)的为优秀.
(1)试分析估计两个班级的优秀率;
(2)由以上统计列出2×2列联表.
某校在高二年级开设了 ,
,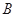 ,
, 三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从
三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从 ,
,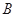 ,
, 三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
| 兴趣小组 | 小组人数 | 抽取人数 |
 | 12 | 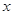 |
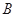 | 36 | 3 |
 | 48 | 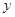 |
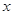 ,
,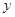 的值;
的值;(2)若从
 ,
,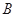 两个兴趣小组所抽取的人中选2人作专题发言,求这2人都来自兴趣小组
两个兴趣小组所抽取的人中选2人作专题发言,求这2人都来自兴趣小组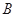 的概率.
的概率. 我市某高中的一个综合实践研究小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差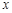 (°C) (°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 (个) (个) | 22 | 25 | 29 | 26 | 16 | 12 |
该综合实践研究小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出
 关于
关于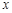 的线性回归方程
的线性回归方程 .
.(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
参考数据:
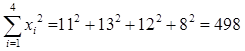 ;
;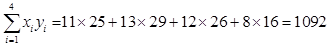 .
. 某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如下表所示.已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16.
| | 第一批次 | 第二批次 | 第三批次 |
| 女教职工 | 196 | x | y |
| 男教职工 | 204 | 156 | z |
(1)求x的值;
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查,问应在第三批次中抽取教职工多少名?

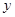 与价格
与价格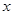 之间有较好的线性相关关系,其线性回归直线方程是;
之间有较好的线性相关关系,其线性回归直线方程是;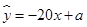
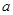 的值;
的值;
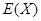 及方差
及方差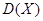 .
. 元/张
元/张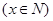 ,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少
,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少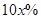 ,“铁杆足球迷”愿意前往观看的人数会减少
,“铁杆足球迷”愿意前往观看的人数会减少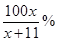 .问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
.问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?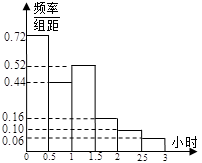
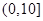 ,第2组
,第2组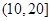 ,第3组
,第3组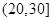 ,第4组
,第4组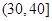 ,第5组
,第5组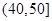 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示. 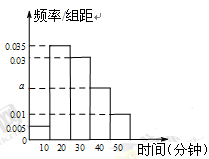
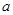 的值
的值