题目内容
已知△ABC的面积为 ,A,B,C所对边分别为a,b,c,且(c+b)(c-b)=a(a+b),
,A,B,C所对边分别为a,b,c,且(c+b)(c-b)=a(a+b),
(1)求角C的大小;
(2)若△ABC的外接圆半径为2,求a+b.
解:(1)∵(c+b)(c-b)=a(a+b),
∴c2-b2=a2+ab
∴a2+b2-c2=-ab
∴cosC= =-
=-
∵0<C<π,∴C= ;
;
(2)∵△ABC的面积为 ,∴ab=4
,∴ab=4
∵△ABC的外接圆半径为2,∴c=2RsinC=
∴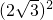 =a2+b2+ab=(a+b)2-ab
=a2+b2+ab=(a+b)2-ab
∴(a+b)2=12+ab=16
∴a+b=4.
分析:(1)利用(c+b)(c-b)=a(a+b),结合余弦定理,可求角C的大小;
(2))由△ABC的面积为 ,可求ab=4,利用△ABC的外接圆半径为2,可求c的值,再利用余弦定理,即可求得结论.
,可求ab=4,利用△ABC的外接圆半径为2,可求c的值,再利用余弦定理,即可求得结论.
点评:本题考查解三角形,考查余弦定理的运用,考查三角形面积的计算,考查学生的计算能力,属于中档题.
∴c2-b2=a2+ab
∴a2+b2-c2=-ab
∴cosC=
 =-
=-
∵0<C<π,∴C=
 ;
;(2)∵△ABC的面积为
 ,∴ab=4
,∴ab=4∵△ABC的外接圆半径为2,∴c=2RsinC=

∴
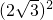 =a2+b2+ab=(a+b)2-ab
=a2+b2+ab=(a+b)2-ab∴(a+b)2=12+ab=16
∴a+b=4.
分析:(1)利用(c+b)(c-b)=a(a+b),结合余弦定理,可求角C的大小;
(2))由△ABC的面积为
 ,可求ab=4,利用△ABC的外接圆半径为2,可求c的值,再利用余弦定理,即可求得结论.
,可求ab=4,利用△ABC的外接圆半径为2,可求c的值,再利用余弦定理,即可求得结论.点评:本题考查解三角形,考查余弦定理的运用,考查三角形面积的计算,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使 (2012•温州一模)如图,在△ABC中,AD⊥BC,垂足为D,且BD:DC:AD=2:3:6.
(2012•温州一模)如图,在△ABC中,AD⊥BC,垂足为D,且BD:DC:AD=2:3:6.