题目内容
某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧 以及两条线段
以及两条线段 和
和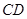 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 所在圆的半径为10米.设小圆弧
所在圆的半径为10米.设小圆弧 所在圆的半径为
所在圆的半径为 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.

(1)求 关于
关于 的函数关系式;
的函数关系式;
(2)在对花坛的边缘进行装饰时,已知两条线段的装饰费用为4元/米,两条弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为 ,当
,当 为何值时,
为何值时, 取得最大值?
取得最大值?
 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧 以及两条线段
以及两条线段 和
和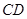 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 所在圆的半径为10米.设小圆弧
所在圆的半径为10米.设小圆弧 所在圆的半径为
所在圆的半径为 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.
(1)求
 关于
关于 的函数关系式;
的函数关系式;(2)在对花坛的边缘进行装饰时,已知两条线段的装饰费用为4元/米,两条弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为
 ,当
,当 为何值时,
为何值时, 取得最大值?
取得最大值?(1) ;(2)参考解析
;(2)参考解析
 ;(2)参考解析
;(2)参考解析试题分析:(1)由于花坛设计周长为30米,其中大圆弧
 所在圆的半径为10米.设小圆弧
所在圆的半径为10米.设小圆弧 所在圆的半径为
所在圆的半径为 米(
米( ),圆心角为
),圆心角为 弧度.所以AD的弧长为
弧度.所以AD的弧长为 ,BC的弧长为
,BC的弧长为 .所以可得
.所以可得 .即可得结论.
.即可得结论.(2)由花坛两条线段的装饰费用为4元/米,两条弧线部分的装饰费用为9元/米.即可得所需费用的关系式. 花坛的面积由大扇形面积减去小的扇形面积即可,再利用基本不等式即可求得结论.
试题解析:(1)设扇环的圆心角为q,则
 ,
,所以
 ,
,(2)花坛的面积为
 .
.装饰总费用为
 ,
,所以花坛的面积与装饰总费用的比
 ,
,令
 ,则
,则 ,当且仅当t=18时取等号,
,当且仅当t=18时取等号,此时
 .
.答:当
 时,花坛的面积与装饰总费用的比最大.
时,花坛的面积与装饰总费用的比最大.
练习册系列答案
相关题目
 残骸,我国“雪龙号”科考船于2014年3月26日从港口
残骸,我国“雪龙号”科考船于2014年3月26日从港口 出发,沿北偏东
出发,沿北偏东 角的射线
角的射线 方向航行,而在港口北偏东
方向航行,而在港口北偏东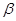 角的方向上有一个给科考船补给物资的小岛
角的方向上有一个给科考船补给物资的小岛 ,
, 海里,且
海里,且
 .现指挥部需要紧急征调位于港口
.现指挥部需要紧急征调位于港口 海里的
海里的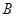 处的补给船,速往小岛
处的补给船,速往小岛 方向全速追赶科考船,并在
方向全速追赶科考船,并在 处相遇.经测算当两船运行的航线与海岸线
处相遇.经测算当两船运行的航线与海岸线 围成的三角形
围成的三角形 的面积
的面积 最小时,这种补给方案最优.
最小时,这种补给方案最优.
 ;
; .
. 在
在 上的最大值和最小值;
上的最大值和最小值;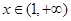 时,函数
时,函数 的下方.
的下方. .
. 对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.
对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围. 的图像与函数
的图像与函数 的图像所有交点的横坐标之和等于
的图像所有交点的横坐标之和等于 ,若存在区间
,若存在区间 ,使得
,使得 ,则称函数
,则称函数 为函数
为函数 ;②
;② ; ③
; ③ ; ④
; ④ .
. 若有一个正实根,一个负实根,则
若有一个正实根,一个负实根,则 ;
; 是偶函数,但不是奇函数;
是偶函数,但不是奇函数; 的值域是
的值域是 ,则函数
,则函数 的值域为
的值域为 ;
; 和直线
和直线 的公共点个数是
的公共点个数是 ,则
,则 .
.