题目内容
3.(2-$\frac{3}{x}$)(x2+$\frac{2}{x}$)5的展开式的常数项为-240.分析 (x2+$\frac{2}{x}$)5的展开式的通项公式:Tr+1=${∁}_{5}^{r}$(x2)5-r$(\frac{2}{x})^{r}$=2r${∁}_{5}^{r}$x10-3r,r=0,1,…,5.令10-3r=0,无解.利用10-3r=1,解得r=3.进而得出答案.
解答 解:(x2+$\frac{2}{x}$)5的展开式的通项公式:Tr+1=${∁}_{5}^{r}$(x2)5-r$(\frac{2}{x})^{r}$=2r${∁}_{5}^{r}$x10-3r,r=0,1,…,5.
令10-3r=0,无解.利用10-3r=1,解得r=3.
∴T4=${2}^{3}{∁}_{5}^{3}$•x,
∴(2-$\frac{3}{x}$)(x2+$\frac{2}{x}$)5的展开式的常数项为:-3×${2}^{3}{∁}_{5}^{3}$=-240,
故答案为:-240.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
8.计算sin47°cos17°+cos47°cos107°的结果等于( )
| A. | $-\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
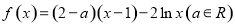 .
. 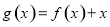 上点
上点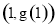 处的切线过点
处的切线过点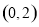 ,求函数
,求函数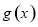 的单调减区间;
的单调减区间; 在
在 上无零点,求
上无零点,求 的最小值.
的最小值.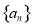 的前
的前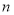 项和为
项和为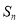 ,已知
,已知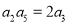 ,且
,且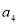 与
与 的等差中项为
的等差中项为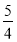 ,则
,则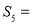 ( )
( ) 中,
中, 为等边三角形,边长为
为等边三角形,边长为 ,
, 面
面 ,
, ,则此三棱锥的外接球的表面积为( )
,则此三棱锥的外接球的表面积为( ) B.
B. C.
C. D.
D.
 ,则“
,则“ ”是“直线
”是“直线 与直线
与直线 平行”的( )
平行”的( ) 如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=AE=2.
如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=AE=2.