题目内容
平面内有向量
=（1，7），
=（5，1），
=（2，1），点Q为直线OP上的一个动点．（1）当
·
取最小值时，求
的坐标；
（2）当点Q满足（1）的条件和结论时，求cos∠AQB的值．
解：（1）设=（x，y），∵Q在直线上，?∴向量与共线.又OP=（2，1），∴x-2y=0 ∴x=2y.?∴=（2y，y）.?又?=
-
=（1-2y，7-y），
=
-
=（5-2y，1-y），?∴?
·
=（1-2y）（5-2y）+（7-y）（1-y）=5y2-20y+12=5（y-2）2-8.?故当y=2时，
·
有最小值-8，此时
=（4，2）.?（2）由（1）知
=（-3，5），
=（1，-1），
·
=-8，｜
?｜=
，｜
｜=
，
∴cosAQB=
.
练习册系列答案
相关题目
=(1,7),
=(5,1),
=(2,1),点X为直线OP上的一动点.
·
取最小时,求
的坐标;
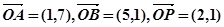，点M为直线OP上的一个动点．
取得最小值时，求点M的坐标；
的余弦值．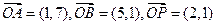
，点X为直线OP上的一动点。
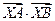取最小值时，求
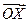的坐标；
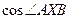的值.