题目内容
已知函数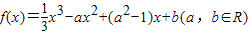 ,
,(1)若x=1为f(x)的极值点,求a的值;
(2)若y=f(x)的图象在点(1,f(1))处的切线方程为x+y-3=0,求f(x)在区间[-2,4]上的最大值;
(3)当a≠0时,若f(x)在区间(-1,1)上不单调,求a的取值范围.
【答案】分析:(1)先求导数,再根据x=1是f(x)的极值点得到:“f′(1)=0”,从而求得a值;
(2)先根据切线方程为x+y-3=0利用导数的几何意义求出a值,再研究闭区间上的最值问题,先求出函数的极值,比较极值和端点处的函数值的大小,最后确定出最大值与最小值.
(3)由题意得:函数f(x)在区间(-1,1)不单调,所以函数f′(x)在(-1,1)上存在零点.再利用函数的零点的存在性定理得:f′(-1)f′(1)<0.由此不等式即可求得a的取值范围.
解答:解:(1)f′(x)=x2-2ax+a2-1
∵x=1是f(x)的极值点,
∴f′(1)=0,即a2-2a=0,解得a=0或2;(3分)
(2)∵(1,f(1))在x+y-3=0上.∴f(1)=2
∵(1,2)在y=f(x)上,∴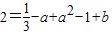 又f′(1)=-1,
又f′(1)=-1,
∴1-2a+a2-1=-1∴a2-2a+1=0,
解得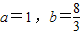 ∴
∴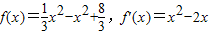
由f′(x)=0可知x=0和x=2是极值点.
∵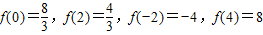
∴f(x)在区间[-2,4]上的最大值为8.(8分)
(3)因为函数f(x)在区间(-1,1)不单调,
所以函数f′(x)在(-1,1)上存在零点.
而f′(x)=0的两根为a-1,a+1,区间长为2,
∴在区间(-1,1)上不可能有2个零点.
所以f′(-1)f′(1)<0,∵a2>0,
∴(a+2)(a-2)<0,-2<a<2.
又∵a≠0,∴a∈(-2,0)∪(0,2).(12分)
点评:本小题主要考查利用导数研究函数的单调性、利用导数研究曲线上某点切线方程、函数的最值及其几何意义、函数在某点取得极值的条件等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.
(2)先根据切线方程为x+y-3=0利用导数的几何意义求出a值,再研究闭区间上的最值问题,先求出函数的极值,比较极值和端点处的函数值的大小,最后确定出最大值与最小值.
(3)由题意得:函数f(x)在区间(-1,1)不单调,所以函数f′(x)在(-1,1)上存在零点.再利用函数的零点的存在性定理得:f′(-1)f′(1)<0.由此不等式即可求得a的取值范围.
解答:解:(1)f′(x)=x2-2ax+a2-1
∵x=1是f(x)的极值点,
∴f′(1)=0,即a2-2a=0,解得a=0或2;(3分)
(2)∵(1,f(1))在x+y-3=0上.∴f(1)=2
∵(1,2)在y=f(x)上,∴
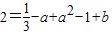 又f′(1)=-1,
又f′(1)=-1,∴1-2a+a2-1=-1∴a2-2a+1=0,
解得
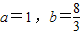 ∴
∴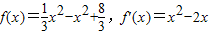
由f′(x)=0可知x=0和x=2是极值点.
∵
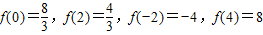
∴f(x)在区间[-2,4]上的最大值为8.(8分)
(3)因为函数f(x)在区间(-1,1)不单调,
所以函数f′(x)在(-1,1)上存在零点.
而f′(x)=0的两根为a-1,a+1,区间长为2,
∴在区间(-1,1)上不可能有2个零点.
所以f′(-1)f′(1)<0,∵a2>0,
∴(a+2)(a-2)<0,-2<a<2.
又∵a≠0,∴a∈(-2,0)∪(0,2).(12分)
点评:本小题主要考查利用导数研究函数的单调性、利用导数研究曲线上某点切线方程、函数的最值及其几何意义、函数在某点取得极值的条件等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. .
. .
. ,求f(x)的值域.
,求f(x)的值域. ,
, 取得极值,求实数
取得极值,求实数 的值;
的值; 时,求
时,求 上的最小值;
上的最小值; ,直线
,直线 都不是曲线
都不是曲线 的切线,求实数
的切线,求实数