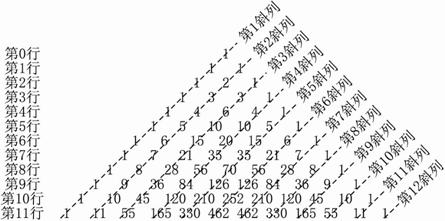
题目内容
(1)项数为奇数的等差数列{an}中,所有奇数项之和为20,所以偶数项之和为15,求这个数列的项数及中间一项;(2)一个等差数列的前12项和为354,前12项中偶数项和与奇数项和之比为32∶27.求公差d.
思路解析:根据等差数列前n项和公式列出方程组求解.注意等差数列性质的运用. 解:(1)设数列共有2n+1项,首项为a1,公差为d,其中奇数项共有n+1项,偶数项共有n项,中间一项是第n+1项.则有 因此,数列共有7项,中间一项是a4=5. (2)解法一:设此数列首项为a1,公差为d,则 12a1+ 解①②组成的方程组,得d=5. 解法二: 又S奇-S偶=6d,∴d=5. 深化升华 本题运用了方程的数学思想方法. 等差数列奇、偶数项与中间项的关系: (1)若等差数列共有2n+1项, 则①S奇= S偶= ②S2n+1=(2n+1)·an+1. (2)若等差数列共有2n项, 则①S奇-S偶=nd; ② ③中间共两项an,an+1,S2n=n(an+an+1).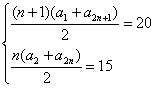
![]()
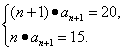 解得an+1=5,n=3.
解得an+1=5,n=3.![]() d=354. ①
d=354. ①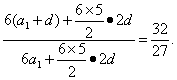 ②
②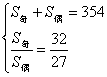
![]()

![]() =(n+1)·an+1,
=(n+1)·an+1,![]() =n·an+1.
=n·an+1.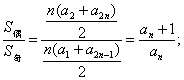

1加1阅读好卷系列答案
专项复习训练系列答案
初中语文教与学阅读系列答案

完形填空与阅读理解周秘计划系列答案
英语阅读理解150篇系列答案
奔腾英语系列答案
标准阅读系列答案
53English系列答案
考纲强化阅读系列答案