题目内容
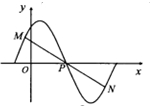 如图,在函数f(x)=Asin(x+φ)的图象中,M、N、P三点共线,M、N两点坐标分别为(x0,y0),(
如图,在函数f(x)=Asin(x+φ)的图象中,M、N、P三点共线,M、N两点坐标分别为(x0,y0),(| 2π |
| 3 |
A、f(x)=2sin(2x+
| ||
B、f(x)=2sin(2x+
| ||
C、f(x)=2sin(2x-
| ||
D、f(x)=2sin(2x-
|
分析:根据条件确定P的坐标,利用三角函数的图象和性质 即可得到结论.
解答:解:由图象可知P是三角函数的一个对称中心,
∵M、N两点坐标分别为(x0,y0),(
-x0,-y0),
∴P(
,0),
将x=
分别代入得:
A.f(
)=2sin(2×
+
)=2sinπ=0,满足条件.
B.f(
)=2sin(2×
+
)=2sin
≠0,不满足条件.
C.f(
)=2sin(2×
-
)=2sin
≠0,不满足条件.
D.f(
)=2sin(2×
-
)=-2sin
≠0,不满足条件.
故选:A
∵M、N两点坐标分别为(x0,y0),(
| 2π |
| 3 |
∴P(
| π |
| 3 |
将x=
| π |
| 3 |
A.f(
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
B.f(
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| 4π |
| 3 |
C.f(
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
D.f(
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
| π |
| 6 |
故选:A
点评:本题主要考查三角函数的图象和性质,根据条件求出对称中心P的坐标是解决本题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
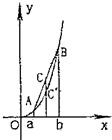 如图,对于函数f(x)=x3(x>0)上任意两点A(a,a3),B(b,b3)线段AB在弧线段AB的上方,
如图,对于函数f(x)=x3(x>0)上任意两点A(a,a3),B(b,b3)线段AB在弧线段AB的上方, 如图,对于函数f(x)=x2(x>0)的图象上不同两点A(a,a2)、B(b,b2),直线段AB
如图,对于函数f(x)=x2(x>0)的图象上不同两点A(a,a2)、B(b,b2),直线段AB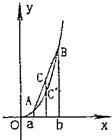
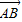 的比为λ(λ>0),则由图象中点C在点C'上方可得不等式
的比为λ(λ>0),则由图象中点C在点C'上方可得不等式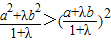 .请分析函数y=lnx(x>0)的图象,类比上述不等式,可以得到的不等式是 .
.请分析函数y=lnx(x>0)的图象,类比上述不等式,可以得到的不等式是 .