题目内容
(本小题12分)如图,设抛物线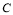 :
: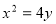 的焦点为F,
的焦点为F,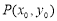 为抛物线上的任一点(其
为抛物线上的任一点(其
中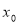 ≠0),过P点的切线交
≠0),过P点的切线交 轴于
轴于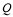 点.
点.
(1)若 ,求证
,求证 ;
;
(2)已知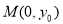 ,过M点且斜率为
,过M点且斜率为 的直线与抛物线
的直线与抛物线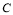 交于A、B两点,若
交于A、B两点,若 ,求
,求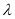 的值.
的值.
(1)证明见解析,(2)
【解析】
试题分析:要证明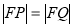 ,由
,由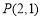 在抛物线上,利用焦半径公式
在抛物线上,利用焦半径公式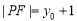 求出,过点
求出,过点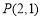 斜率为
斜率为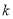 的直线可设为点斜式,与抛物线联立,由于相切,则可借助判别式为0,求出
的直线可设为点斜式,与抛物线联立,由于相切,则可借助判别式为0,求出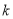 ,得出切线方程,再找出切线与
,得出切线方程,再找出切线与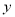 轴的交点
轴的交点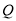 ,进而求出
,进而求出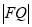 ,得出所证的结论.(2)利用点斜式写出直线方程
,得出所证的结论.(2)利用点斜式写出直线方程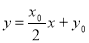 ,与抛物线方程联立消去
,与抛物线方程联立消去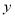 后,得到关于
后,得到关于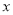 的一元二次方程,于是得出
的一元二次方程,于是得出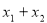 和
和 ,通过
,通过 找出
找出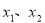 的关系,代入
的关系,代入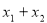 和
和 即可就出
即可就出 .
.
试题解析:(Ⅰ)证明:由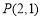 在抛物线上,利用抛物线定义知
在抛物线上,利用抛物线定义知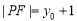
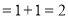
设过P点的切线方程为 ,由
,由
 ,
,
令 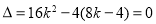 得
得 ,切线方程
,切线方程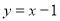 ,
,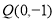 ,∴
,∴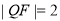 ,即 |PF|=|QF|;
,即 |PF|=|QF|;
(Ⅱ)设A(x1, y1),B(x2, y2),又M点坐标为(0, y0) ∴AB方程为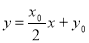 ,由
,由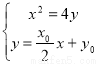 得
得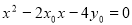 ,∴
,∴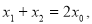
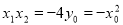 ……① ,由
……① ,由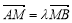 得:
得:
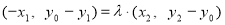 ,∴
,∴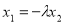 ……② , 由①②知
……② , 由①②知 ,
,
得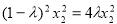 ,由
,由 可得
可得 ,∴
,∴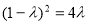 ,又
,又 ,解得:
,解得: .
.
考点:1.抛物线定义;2.焦半径公式;3.直线方程的点斜式;3.设而不求思想;4.一元二次方程的根与系数关系;5.代入减元思想;

练习册系列答案
相关题目

 的图像。
的图像。 与
与 有3个交点,求k的值;
有3个交点,求k的值; 有两个不等实根,则实数
有两个不等实根,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 在正方体
在正方体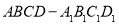 的对角线
的对角线 上,过点
上,过点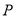 作垂直于平面
作垂直于平面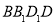 的直线,与正方体表面相交于
的直线,与正方体表面相交于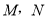 .设
.设 ,
, ,则函数
,则函数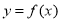 的图象大致是 ( )
的图象大致是 ( )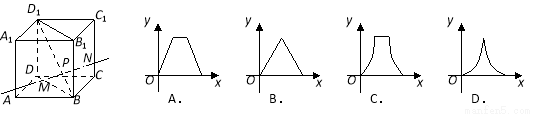
 与圆
与圆 有公共点,则( )
有公共点,则( ) B.
B. C.
C. D.
D.
 与直线
与直线 交于A,B两点,若
交于A,B两点,若 ,则过原点与线段AB的中点M的连线的斜率为 .
,则过原点与线段AB的中点M的连线的斜率为 .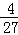 B.
B.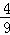 C.
C.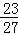 D.
D.
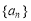 前
前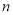 项和为
项和为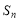 ,则下列一定成立的是
,则下列一定成立的是 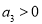 ,则
,则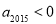 B.若
B.若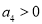 ,则
,则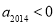
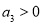 ,则
,则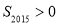 D.若
D.若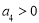 ,则
,则