题目内容
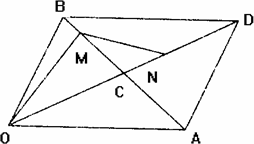
如图所示,已知四边形ABCD、EADM和MDCF都是边长为a的正方形,点P、Q分别是ED和AC的中点.求:
(1) ![]() 与
与![]() 所成的角;
所成的角;
(2)P点到平面EFB的距离;
(3)异面直线PM与FQ的距离.
解:建立空间直角坐标系,使得D(0,0,0)、A(a,0,0)、B(a,a,0)、C(0,a,0)、M(0,0,a)、E(a,0,a)、F(0,a,a),则由中点坐标公式得P(![]() ,0,
,0,![]() )、Q(
)、Q(![]() ,
,![]() ,0).
,0).
(1)∴![]() =(-
=(-![]() ,0,
,0,![]() ),
), ![]() =(
=(![]() ,-
,-![]() ,-a),
,-a), ![]() ·
·![]() =(-
=(-![]() )×
)×![]() +0+
+0+![]() ×(-a)=
×(-a)=![]() a2,
a2,
且|![]() |=
|=![]() a,|
a,| ![]() |=
|=![]() a.
a.
∴cos〈![]() ,
,![]() 〉=
〉= =
= =-
=-![]() .
.
故得两向量所成的角为150°.
(2)设n=(x,y,z)是平面EFB的单位法向量,即|n|=1,n⊥平面EFB,
∴n⊥![]() ,n⊥
,n⊥![]() .又
.又![]() =(-a,a,0),EB=(0,a,-a),即有
=(-a,a,0),EB=(0,a,-a),即有 得其中的一组解
得其中的一组解
∴n=(![]() ,
,![]() ,
,![]() ),
),![]() =(
=(![]() ,0,
,0,![]() ).
).
设所求距离为d,则d=|![]() ·n|=
·n|=![]() a.
a.
(3)设e=(x1,y1,z1)是两异面直线的公垂线上的单位方向向量,则由![]() =(-
=(-![]() ,0,
,0,![]() ),
), ![]() =(
=(![]() ,-
,-![]() ,-a),得
,-a),得
 求得其中的一个e=(
求得其中的一个e=(![]() ,-
,-![]() ,
,![]() ),而
),而![]() =(0,a,0).
=(0,a,0).
设所求距离为m,则m=|![]() ·e|=|-
·e|=|-![]() a|=
a|=![]() a.
a.

练习册系列答案
相关题目