题目内容
已知幂函数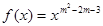 (
(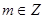 )在
)在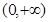 是单调减函数,且为偶函数.
是单调减函数,且为偶函数.
(1)求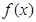 的解析式;
的解析式;
(2)讨论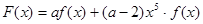 的奇偶性,并说明理由.
的奇偶性,并说明理由.
(1) ;(2)详见解析.
;(2)详见解析.
解析试题分析:(Ⅰ)由幂函数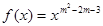 (
(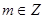 )在
)在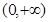 是单调减函数,且为偶函数可知
是单调减函数,且为偶函数可知 ,得
,得 ,又因为
,又因为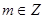 所以
所以 ;
;
(Ⅱ)由(Ⅰ)求出 ,对参数a进行讨论,再利用函数的奇偶性判断方法进行判断.
,对参数a进行讨论,再利用函数的奇偶性判断方法进行判断.
试题解析:(1)由于幂函数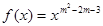 在
在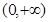 是单调减函数,
是单调减函数,
所以 1分
1分
求得 因为
因为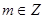 ,所以
,所以 2分
2分
因为 是偶函数,所以
是偶函数,所以 3分
3分
故: 4分
4分
(2)

 6分
6分
 8分
8分
当 ,因为
,因为 ,
, ,
, 9分
9分 . 10分.
. 10分.
考点:1.幂函数的性质;2.函数的奇偶性.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 .
. 其对应曲线(如图所示)过点
其对应曲线(如图所示)过点 .
. 
 (a为常数)在x=1处的切线的斜率为1.
(a为常数)在x=1处的切线的斜率为1.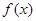 的单调区间,
的单调区间,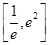 上恒成立,其中e为自然对数的底数,求实数k的取值范围.
上恒成立,其中e为自然对数的底数,求实数k的取值范围. 的定义域是
的定义域是 ,对于任意的
,对于任意的 ,有
,有 ,且当
,且当 时,
时, .
. 的值;
的值; 为增函数;
为增函数; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 上的函数
上的函数 同时满足以下条件:
同时满足以下条件: 在(0,1)上是减函数,在(1,+∞)上是增函数;
在(0,1)上是减函数,在(1,+∞)上是增函数; 是偶函数;
是偶函数; y=x+2垂直.
y=x+2垂直. =
= ,若存在实数x∈[1,e],使
,若存在实数x∈[1,e],使 <
< 对任意实数
对任意实数 均有
均有 ,且当
,且当 时,
时,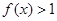 .
.
 时,解不等式
时,解不等式
 .
. ,试判断
,试判断 在定义域内的单调性;
在定义域内的单调性; 时,若
时,若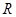 上有
上有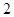 个零点,求
个零点,求 的取值范围.
的取值范围. 满足
满足 ,当
,当 时,
时,
 ,当
,当 时,
时, 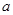 的值;
的值;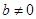 ,函数
,函数 ,
, .若对任意的
.若对任意的 ,总存在
,总存在 ,使
,使 ,求实数
,求实数 的取值范围.
的取值范围.