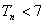题目内容
已知二次函数![]() (
(![]()
![]() R,
R,![]()
![]() 0).
0).
(Ⅰ)当0<![]() <
<![]() 时,
时,![]() (
(![]()
![]() R)的最大值为
R)的最大值为![]() ,求
,求![]() 的最小值.
的最小值.
(Ⅱ)如果![]() [0,1]时,总有|
[0,1]时,总有|![]() |
|![]() .试求
.试求![]() 的取值范围.
的取值范围.
(Ⅲ)令![]() ,当
,当![]() 时,
时,![]() 的所有整数值的个数为
的所有整数值的个数为![]() ,求数列
,求数列![]() 的前
的前![]() 项的和
项的和![]() .
.
(1)最大值为![]() 最小值为
最小值为![]() (2)
(2)![]() (3)
(3)![]()
解析:
⑴ 由![]() 知
知![]() 故当
故当![]() 时
时![]() 取得最大值为
取得最大值为![]() ,
,
即![]() ,所以
,所以![]() 的最小
的最小
值为![]() ;
;
⑵ 由![]() 得
得![]()
![]() 对于任意
对于任意![]() 恒成立,
恒成立,
当![]() 时,
时,![]() 使
使![]() 成立;
成立;
|

对于任意的![]() 恒成立;
恒成立;![]() ,则
,则![]() ,故要使①式成立,则有
,故要使①式成立,则有![]() ,又
,又![]() ;又
;又![]() ,则有
,则有![]() ,综上所述:
,综上所述:![]() ;
;
⑶ 当![]() 时,
时,![]() ,则此二次函数的对称轴为
,则此二次函数的对称轴为![]() ,开口向上,
,开口向上,
故![]() 在
在![]() 上为单调递增函数,且当
上为单调递增函数,且当![]() 时,
时,![]() 均为整数,
均为整数,
故![]() ,
,
则数列![]() 的通项公式为
的通项公式为![]() ,故
,故![]() ①
①
又![]() ②
②
由①—②得![]() .
.
![]()

练习册系列答案
相关题目
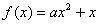 (
(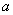
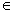 R,
R,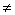 0).
0).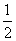 时,
时,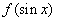 (
(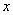
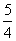 ,求
,求 的最小值.
的最小值.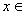 [0,1]时,总有|
[0,1]时,总有|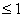 .试求
.试求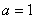 ,当
,当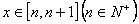 时,
时,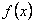 的所有整数值的个数为
的所有整数值的个数为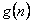 ,求证数列
,求证数列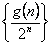 的前
的前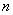 项的和
项的和