题目内容
(I)试证明柯西不等式: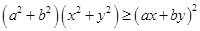
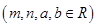
(II)已知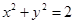 ,且
,且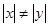 ,求
,求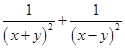 的最小值.
的最小值.
【答案】
(1)对于不等式的证明可以运用综合法也可以运用分析法来得到。也可以运用作差法加以证明。
(2)根据题意,由于 ,那么结合均值不等式来求解最值。
,那么结合均值不等式来求解最值。
【解析】
试题分析:(Ⅰ)证明:左边= ,
,
右边= ,
,
左边 右边
右边 , 2分
, 2分
 左边
左边 右边, 命题得证. 3分
右边, 命题得证. 3分
(Ⅱ)令 ,则
,则 ,
,
 ,
,  ,
,
 ,
4分
,
4分
由柯西不等式得: , 5分
, 5分
当且仅当 ,即
,即 ,或
,或 时
6分
时
6分
 的最小值是1
. 7分
的最小值是1
. 7分
解法2: ,
, ,
,
 ,
4分
,
4分
 , 5分
, 5分
当且仅当 ,或
,或 时 6分
时 6分
 的最小值是1. 7分
的最小值是1. 7分
考点:不等式的证明与求解最值
点评:主要是考查了不等式的证明,以及均值不等式求解最值的运用,属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


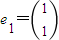 是矩阵
是矩阵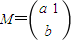 属于特征值λ1=2的一个特征向量.
属于特征值λ1=2的一个特征向量.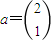 ,求M10a.
,求M10a. 为参数).
为参数). |为长度单位,射线AB为极轴建立极坐标系,求曲线C的极坐标方程.
|为长度单位,射线AB为极轴建立极坐标系,求曲线C的极坐标方程. 的最小值.
的最小值.