Question

本小题设有（1）（2）（3）三个选考题，每题7分，请考生任选两题作答，满分14分，如果多做，则按所做的前两题计分．
（1）选修4-2：矩阵与变换
已知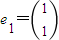是矩阵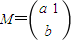属于特征值λ₁=2的一个特征向量．
（I）求矩阵M；
（Ⅱ）若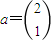，求M¹⁰a．
（2）选修4-4：坐标系与参数方程
在平面直角坐标系xOy中，A（l，0），B（2，0）是两个定点，曲线C的参数方程为为参数）．
（I）将曲线C的参数方程化为普通方程；
（Ⅱ）以A（l，0为极点，||为长度单位，射线AB为极轴建立极坐标系，求曲线C的极坐标方程．
（3）选修4-5：不等式选讲
（I）试证明柯西不等式：（a²+b²）（x²+y²）≥（ax+by）²（a，b，x，y∈R）；
（Ⅱ）若x²+y²=2，且|x|≠|y|，求的最小值．

Answer 1

【答案】分析：（1）（I）由题意，根据特征值与特征向量的定义，建立方程组，即可求得矩阵M；
（Ⅱ）求出矩阵M的特征多项式为f（λ）=（λ-1）（λ-2），从而可求矩阵M的另一个特征值与特征向量，将向量用特征向量线性表示，进而可求结论；
（2）（I）由消去θ，即可得普通方程；
（Ⅱ）将原点移至A（1，0），则相应曲线C的方程为（x-1）²+y²=1，从而可得曲线C的极坐标方程；
（3）（I）利用作差法即可证得；
（Ⅱ）令u=x+y，v=x-y，则，根据，可得u²+v²=4，由柯西不等式得：，从而可求的最小值．
解答：（1）解：（I）由题意，，∴，∴a=1，b=2
∴矩阵M=；
（Ⅱ）由（I）知，矩阵M的特征多项式为f（λ）=（λ-1）（λ-2）
∴矩阵M的另一个特征值为λ₂=1
设是矩阵M属于特征值1的特征向量，则
∴，取x=1，则
∴
∴=
（2）（I）由消去θ可得（x-2）²+y²=1；
（Ⅱ）将原点移至A（1，0），则相应曲线C的方程为（x-1）²+y²=1，即x²+y²-2x=0
∴曲线C的极坐标方程为ρ-2cosθ=0
（3）（I）证明：左边-右边=a²y²+b²x²-2abxy=（ay-bx）²≥0，∴左边≥右边
即
（Ⅱ）令u=x+y，v=x-y，则
∵，∴（u+v）²+（u-v）²=8，∴u²+v²=4
由柯西不等式得：，当且仅当，即或时，的最小值是1．
点评：本题是选做题，考查矩阵的性质和应用、特征值与特征向量的计算，考查坐标系与参数方程，考查柯西不等式的证明与运用，属于中档题．