题目内容
已知定义在
上的偶函数
，当
时，
，那么
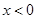时，
_____.
解析试题分析：先由函数是偶函数得
，然后将所求区间利用运算转化到已知区间上，代入到时，，即可的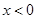时，函数的解析式．这类题一般是求那一部设那一部分.
当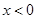时则
因为是偶函数,所以
所以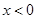时，
考点：函数解析式的求解及常用方法；函数奇偶性的性质．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
小学学习好帮手系列答案小学同步三练核心密卷系列答案题目内容
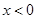已知定义在上的偶函数，当时，，那么时，_____.
解析试题分析：先由函数是偶函数得，然后将所求区间利用运算转化到已知区间上，代入到时，，即可的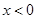时，函数的解析式．这类题一般是求那一部设那一部分.
当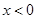时则
因为是偶函数,所以
所以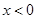时，
考点：函数解析式的求解及常用方法；函数奇偶性的性质．
小学学习好帮手系列答案小学同步三练核心密卷系列答案
的定义域为 ．
是偶函数，则
的递减区间是 .
定义如下面数表，数列
满足
，且对任意自然数
均有
，则
的值为___________________。
，若
、
满足
，且
恒成立，则
的最小值为 .
的最大值是 .
上偶函数，当x
（0，+∞）时，f（x）是单调增函数，且
则
<0的解集为 ．
上的函数
既是偶函数又是周期函数，若
，且当
时，
，则
的值为_________．
，有下列命题：
，则
；
，则
可为奇函数；
，总有
成立．