题目内容
已知an是一个等差数列,且a2=18,a14=-6.
(1)求an的通项an;
(2)求an的前n项和Sn的最大值并求出此时n值.
解:(1)由 (4分)
(4分)
an=22-2n(6分)
(2)∵ ,
,
∴ (8分)
(8分)
Sn=-n2+21n
∴ (10分)
(10分)
∴n=10或11,有最大值S10(S11)=110(12分)
分析:(1)用首项a1及公差d表示a2,a14,联李方程可求a1,d代入等差数列的通项公式即可
(2)由(1)可知a1及公差d,代入等差数列的前n项和公式,利用二次函数的知识可求Sn的最大值及取得最大值n
点评:本题主要考查了利用基本量表示等差数列的通项公式,前n项和,及前n项和取得最值的条件.
 (4分)
(4分)an=22-2n(6分)
(2)∵
 ,
,∴
 (8分)
(8分)Sn=-n2+21n
∴
 (10分)
(10分)∴n=10或11,有最大值S10(S11)=110(12分)
分析:(1)用首项a1及公差d表示a2,a14,联李方程可求a1,d代入等差数列的通项公式即可
(2)由(1)可知a1及公差d,代入等差数列的前n项和公式,利用二次函数的知识可求Sn的最大值及取得最大值n
点评:本题主要考查了利用基本量表示等差数列的通项公式,前n项和,及前n项和取得最值的条件.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
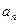 ;(Ⅱ)求{an}前n项和Sn的最大值.
;(Ⅱ)求{an}前n项和Sn的最大值.