题目内容
首项为正数的数列{an}满足an+1=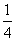 (an2+3),n∈N*,
(an2+3),n∈N*,
(Ⅰ)证明:若a1为奇数,则对一切n≥2,an都是奇数;
(Ⅱ)若对一切n∈N*,都有an+1>an,求a1的取值范围。
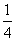 (an2+3),n∈N*,
(an2+3),n∈N*,(Ⅰ)证明:若a1为奇数,则对一切n≥2,an都是奇数;
(Ⅱ)若对一切n∈N*,都有an+1>an,求a1的取值范围。
解:(Ⅰ)已知a1是奇数,假设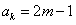 是奇数,其中m为正整数,
是奇数,其中m为正整数,
则由递推关系得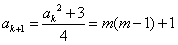 是奇数。
是奇数。
根据数学归纳法,对任何n∈N+,an都是奇数。
(Ⅱ)由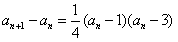 知,
知, ,当且仅当
,当且仅当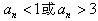 ;
;
另一方面,若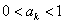 ,则
,则 ;
;
若 ,则
,则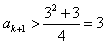 ,
,
根据数学归纳法,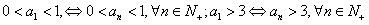 ;
;
综合所述,对一切n∈N+都有 的充要条件是
的充要条件是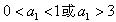 。
。
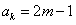 是奇数,其中m为正整数,
是奇数,其中m为正整数,则由递推关系得
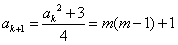 是奇数。
是奇数。根据数学归纳法,对任何n∈N+,an都是奇数。
(Ⅱ)由
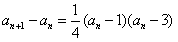 知,
知, ,当且仅当
,当且仅当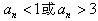 ;
;另一方面,若
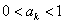 ,则
,则 ;
;若
 ,则
,则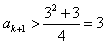 ,
,根据数学归纳法,
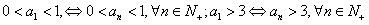 ;
;综合所述,对一切n∈N+都有
 的充要条件是
的充要条件是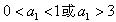 。
。 
练习册系列答案
相关题目
 (an2+3),n∈N+.
(an2+3),n∈N+.