题目内容
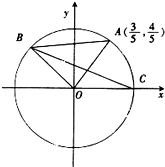 如图,过原点且倾斜角为α的直线交单位圆于点A(
如图,过原点且倾斜角为α的直线交单位圆于点A(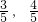 ),C是单位圆与x轴正半轴的交点,B是单位圆上第二象限的点,且△AOB为正三角形.
),C是单位圆与x轴正半轴的交点,B是单位圆上第二象限的点,且△AOB为正三角形.
(I)求sin2 的值;
的值;
(II)求△BOC的面积.
解:(I)由三角函数的定义可知 sinα= ,cosα=
,cosα= ,∴
,∴ =
= =
= .
.
(II)又△AOB为正三角形,∠AOB= ,
,
∴sin∠BOC=sin(α+ )=sinαcos
)=sinαcos +cosαsin
+cosαsin =
= +
+ =
=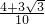 .
.
△BOC的面积等于 OB×OC sin∠BOC=
OB×OC sin∠BOC= =
= .
.
分析:(I)由三角函数的定义可知 sinα= ,cosα=
,cosα= ,可得
,可得  =
= =
= .
.
(II)又△AOB为正三角形,∠AOB= ,求得 sin∠BOC=sin(α+
,求得 sin∠BOC=sin(α+ )=sinαcos
)=sinαcos +cosαsin
+cosαsin 的值,
的值,
由△BOC的面积等于 OB×OC sin∠BOC 求出结果.
OB×OC sin∠BOC 求出结果.
点评:本题考查任意角的三角函数的定义,两角和的正弦公式的应用,求出 sinα= ,cosα=
,cosα= ,是解题的关键.
,是解题的关键.
 ,cosα=
,cosα= ,∴
,∴ =
= =
= .
.(II)又△AOB为正三角形,∠AOB=
 ,
,∴sin∠BOC=sin(α+
 )=sinαcos
)=sinαcos +cosαsin
+cosαsin =
= +
+ =
=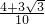 .
.△BOC的面积等于
 OB×OC sin∠BOC=
OB×OC sin∠BOC= =
= .
.分析:(I)由三角函数的定义可知 sinα=
 ,cosα=
,cosα= ,可得
,可得  =
= =
= .
.(II)又△AOB为正三角形,∠AOB=
 ,求得 sin∠BOC=sin(α+
,求得 sin∠BOC=sin(α+ )=sinαcos
)=sinαcos +cosαsin
+cosαsin 的值,
的值,由△BOC的面积等于
 OB×OC sin∠BOC 求出结果.
OB×OC sin∠BOC 求出结果.点评:本题考查任意角的三角函数的定义,两角和的正弦公式的应用,求出 sinα=
 ,cosα=
,cosα= ,是解题的关键.
,是解题的关键. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
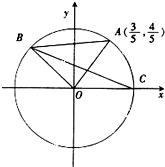 如图,过原点且倾斜角为α的直线交单位圆于点A(
如图,过原点且倾斜角为α的直线交单位圆于点A( (2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
(2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为 (2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
(2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为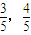 ),C是单位圆与x轴正半轴的交点,B是单位圆上第二象限的点,且△AOB为正三角形.
),C是单位圆与x轴正半轴的交点,B是单位圆上第二象限的点,且△AOB为正三角形. 的值;
的值;