题目内容
【题目】已知椭圆
：在
轴上的一个焦点，与短轴两个端点的连线互相垂直，且右焦点坐标为
．
（1）求椭圆的方程；
（2）设直线
与圆
相切，和椭圆交于
，
两点，
为原点，线段
，
分别和圆交于，
两点，设
，
的面积分别为
，
，求
的取值范围．
【答案】（1）
；（2）
【解析】
（1）设椭圆的标准方程为
，利用待定系数法求解；
（2）分直线
斜率不存在与存在两种情况讨论，当直线斜率不存在时，易得
，当直线斜率存在，设设
，
，由直线与圆相切得到
，将直线与椭圆联立得到韦达定理，将
表示成k的函数，求出值域即可.
（1）设椭圆的标准方程为．
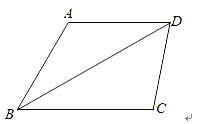
如图所示，
为等腰直角三角形，
为斜边
的中线（高），
且
，
，
，
．
故所求椭圆的标准方程为
（2）①当直线斜率不存在时，其方程为
，由对称性，不妨设为
，
此时
，
，
，
，故
②若直线斜率存在，设其方程为
，由已知得
设，，将直线与椭圆联立得
由韦达定理
，
结合
及
，
可知：
将韦达定理代入整理得
结合知
，设
，
则
综上的取值范围为
【题目】为测试特斯拉汽车的百米加速时间，研发人员记录了汽车在
取
、
、
、
、
、
、
时刻的位移，并对数据做了初步处理，得到图
.同时，令
，得到数据图
，现画出
与，与
的散点图.
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
累加 |
|
|
|
| 累加 |
|
|
|
|
（1）根据散点图判断，与，与哪两个量之间线性相关程度更强？（直接给出判断即可）；
（2）根据（1）的结果选择线性相关程度更强的两个量，建立相应的回归直线方程；
（3）根据（2）的结果预计特斯拉汽车百米加速需要的时间.
附：对于一组数据
、
、
、
，其回归直线
的斜率和截距的最小二乘估计分别为：
，
.
【题目】在2018年俄罗斯世界杯期间,莫斯科的部分餐厅经营了来自中国的小龙虾,这些小龙虾标有等级代码.为得到小龙虾等级代码数值
与销售单价
之间的关系,经统计得到如下数据：
等级代码数值 | 38 | 48 | 58 | 68 | 78 | 88 |
销售单价 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
（1）已知销售单价与等级代码数值之间存在线性相关关系,求关于的线性回归方程(系数精确到0.1)；
（2）若莫斯科某餐厅销售的中国小龙虾的等级代码数值为98，请估计该等级的中国小龙虾销售单价为多少元？
参考公式：对一组数据
,
，····
,其回归直线
的斜率和截距最小二乘估计分别为：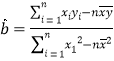
,
.
参考数据：
,
.
