题目内容
在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=1, .
.(1)求证:平面A1BC⊥平面ACC1A1;
(2)如果D为AB的中点,求证:BC1∥平面A1CD.

【答案】分析:(1)利用等边三角形的判定、勾股定理的逆定理、及线面、面面垂直的判定定理和性质定理即可证明;
(2)利用平行四边形的性质、三角形的中位线定理、线面平行的判定定理即可证明.
解答:证明:(1)在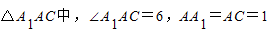 ,∴A1C=1,
,∴A1C=1,
在△A1BC中,BC=1,A1C=1,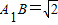 ,∴
,∴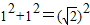 ,∴
,∴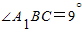 ,∴BC⊥A1C,
,∴BC⊥A1C,
又AA1⊥BC,AA1∩A1C=A1,
∴BC⊥平面ACC1A1,
∵BC?平面A1BC,
∴平面A1BC⊥平面ACC1A1.
(2)连接A1C交AC1于O,连接DO,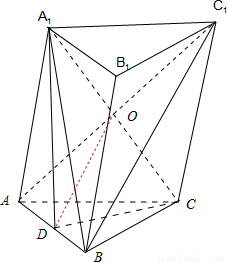
则由D为AB中点,O为AC1中点得,OD∥BC1,
∵OD?平面A1DC,BC1?平面A1DC,
∴BC1∥平面A1DC.
点评:熟练掌握等边三角形的判定、勾股定理的逆定理、及线面、面面垂直与平行的判定定理和性质定理、平行四边形的性质、三角形的中位线定理是证明问题的关键.
(2)利用平行四边形的性质、三角形的中位线定理、线面平行的判定定理即可证明.
解答:证明:(1)在
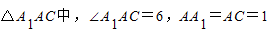 ,∴A1C=1,
,∴A1C=1,在△A1BC中,BC=1,A1C=1,
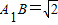 ,∴
,∴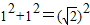 ,∴
,∴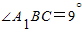 ,∴BC⊥A1C,
,∴BC⊥A1C,又AA1⊥BC,AA1∩A1C=A1,
∴BC⊥平面ACC1A1,
∵BC?平面A1BC,
∴平面A1BC⊥平面ACC1A1.
(2)连接A1C交AC1于O,连接DO,

则由D为AB中点,O为AC1中点得,OD∥BC1,
∵OD?平面A1DC,BC1?平面A1DC,
∴BC1∥平面A1DC.
点评:熟练掌握等边三角形的判定、勾股定理的逆定理、及线面、面面垂直与平行的判定定理和性质定理、平行四边形的性质、三角形的中位线定理是证明问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
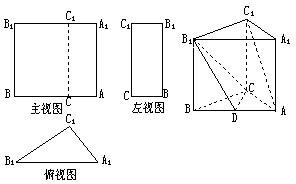 已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5,
已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5, 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
(2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.