Question

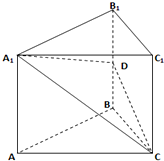如图，在直三棱柱ABC-A₁B₁C₁中，底面△ABC为等腰直角三角形，∠B=90°，D为棱BB₁上一点，且平面DA₁C⊥平面AA₁C₁C．
（1）求证：D点为棱BB₁的中点；
（2）若二面角A-A₁D-C的平面角为60°，求

AA1

AB

的值．

Answer 1

分析：（1）利用同一性证明，先作出AC中点F，DE⊥A₁C于E点，再证明出EF=BD，EF平行且等于AA₁，从而得出BD=

1

2

BB₁即可．
（2）方法一作出相应的辅助线，作出二面角的平面角，利用角为60度建立方程，求出比值．
方法二建立空间坐标系，将两线段的长度转化为坐标，求出两个平面的法向量，利用夹角公式建立方程求出两线段长度之间的比值．

解答：证明：（1）过点D作DE⊥A₁C于E点，取AC的中点F，连BF，EF．
∵面DA₁C⊥面AA₁C₁C且相交于A₁C，面DA₁C内的直线DE⊥A₁C，∴DE⊥面AA₁C₁C．（3分）
又∵面BAC⊥面AA₁C₁C且相交于AC，且△ABC为等腰三角形，易知BF⊥AC，
∴BF⊥面AA₁C₁C．由此知：
DE∥BF，从而有D，E，F，B共面，
又易知BB₁∥面AA₁C₁C，故有DB∥EF，从而有EF∥AA₁，
又点F是AC的中点，所以DB=EF=

1

2

AA1=

1

2

BB1，所以D点为棱BB₁的中点．（6分）

（2）（法一）∵面AA₁B₁B⊥面ABC，面ABC∩面AA₁B₁B=AB，BC⊥AB，
∴BC⊥面AA₁DB，延长A₁D交AB的延长线于点M，过B作BH⊥A₁D交A₁D于点H，连接CH，则CH⊥A₁D，
∴∠CHB为二面角A-A₁D-C的平面角，且∠CHB=60°，（9分）
设A₁A=2b，AB=BC=a，由①易知BD=b，BM=a，
则BH=

BD×BM

DM

=

ab

a2+b2

，
∴tan∠CHB=

BC

BH

=

a

ab a2+b2

=

3

，
∴

b

a

=

2

2

，
∴

A1A

AB

=

2b

a

=

2

（12分）

（法二）建立如图所示直角坐标系，
设AA₁=2b，AB=BC=a，
则D（0，0，b），A₁（a，0，2b），C（0，a，0），
所以

DA1

=(a，0，b)，

DC

=(0，a，-b)，（8分）
设面DA₁C的法向量为

n

=(x，y，z)，则

ax+0•y+bz=0 0•x+ay-bz=0

可取

n

=(b，-b，-a)又
可取平面AA₁DB的法向量

m

=

BC

=(0，a，0)，
cos?

n

，

m

＞=

n • m

| n |•| m |

=

b•0-b•a-a•0

2b2+a2 • a2

=-

b

2b2+a2

（10分）
据题意有：

b

2b2+a2

=

1

2

，
解得：

b

a

=

2

2

所以

AA1

AB

=

2b

a

=

2

（12分）

点评：考查几何证明与二面角的性质，通过第二小题的对比可以看到，用向量法解决此类问题比几何法方便快捷，思维难度大大降低．