Question

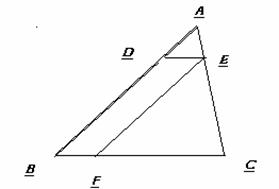
如图1-1-7所示，一个椭圆的长轴长为2a，短轴长为2b，在一直角EOF内滚动，并始终与∠EOF的两边OE、OF分别相切.求椭圆中心O′的轨迹.

图1-1-7

Answer 1

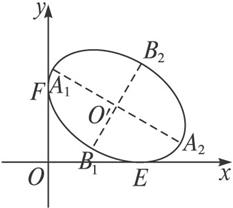
思路分析：由于椭圆相对于直角是运动的，不便找出中心O′相对于直角的变化规律.若反过来变更问题的形式，由于直角与椭圆的动与静是相对的，把椭圆看作是固定的，而与之相切的直角自然就是绕着椭圆转动了.问题就转化为如图所示的“求椭圆=1的两条互相垂直的切线的交点的轨迹”.

解：如图所示，在坐标系xO′y中设两条互相垂直的切线OE、OF的交点O的坐标为(u,v)，当两条切线的斜率都存在时，设椭圆=1的切线的斜率为k，则过点O(u,v)的切线方程为y=k(x-u)+v，将其代入椭圆方程并整理可以得到

(b²+k²a²)x²-2a²(ku-v)x+a²［(ku-v)²-b²］=0.

于是有Δ=［-2a²（ku-v）］²-4(b²+k²a²)·a²［(ku-v)²-b²］=0.

化简得关于k的一元二次方程(u²-a²)k²-2uvk+(v²-b²)=0.

这个关于k的一元二次方程的两个根就是切线OE、OF的斜率.因为OE⊥OF，所以两根之积为-1，即=-1.从而有u²+v²=a²+b².

当两条切线的斜率不都存在时，显然也有u²+v²=a²+b²成立.

这说明椭圆=1的两条互相垂直的切线OE、OF的交点O与椭圆的中心点O′之距恒为定值.再将问题转回到原问题上来，如图所示建立坐标系xOy，则O′的轨迹方程为x²+y²=a²+b²(b≤x≤a且b≤y≤a).