题目内容
(14分)已知数列![]() 满足
满足![]() ,
, ![]() .
.
(Ⅰ)若![]() ,证明数列
,证明数列![]() 为等比数列,并求数列
为等比数列,并求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 对一切
对一切![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围,若不存在,说明理由;
的取值范围,若不存在,说明理由;
解析:(Ⅰ)![]()
![]()

![]() …………………………………6分
…………………………………6分
(Ⅱ)解法1:由![]() ,得
,得![]()
猜想![]() 时,一切
时,一切![]() 时
时![]() 恒成立.
恒成立.
①当![]() 时,
时,![]() 成立.
成立.
②设![]() 时,
时,![]() ,则由
,则由![]()
得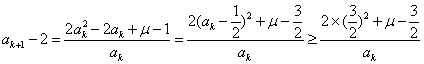 =
=![]()
![]()
![]() 时,
时,![]()
![]() 由①②知
由①②知![]() 时,对一切
时,对一切![]() ,有
,有![]() . ………………………………10分
. ………………………………10分
解法2:假设![]()
![]()
记![]() ,可求
,可求
![]()
故存在![]() ,使
,使![]() 恒成立. …………………………………10分
恒成立. …………………………………10分
(Ⅲ)证法1:![]()
![]() ,由(Ⅱ)知
,由(Ⅱ)知![]()
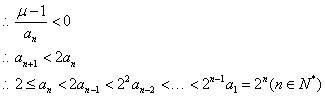
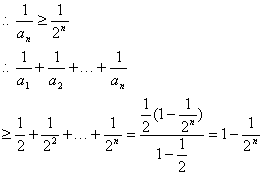
…………………………………14分
证法2:![]()
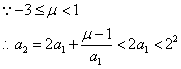
猜想![]() .数学归纳法证明
.数学归纳法证明
①当![]() 时,
时,![]() 成立
成立
②假设当![]() 时,
时,![]() 成立
成立
![]()
![]()
由①②对![]() ,
,![]() 成立,下同证法1。
成立,下同证法1。
…………………………………14分

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 满足
满足 ,则此数列的通项
,则此数列的通项 等于
等于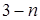 B.
B. C.
C.  D.
D. 
 满足:
满足: .
. ;
; ,求数列
,求数列 的通项公式;
的通项公式; ,不等式
,不等式 恒成立时,求实数
恒成立时,求实数 的取值范围.
的取值范围.