题目内容
设F1、F2是双曲线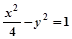 的两个焦点,P在双曲线上,且满足∠F1PF2=90°,则△PF1F2的面积是( )
的两个焦点,P在双曲线上,且满足∠F1PF2=90°,则△PF1F2的面积是( )
| A.1 | B.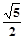 | C.2 | D.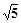 |
A
解析试题分析:设|PF1|=x,|PF2|=y,根据根据双曲线性质可知x-y的值,再根据∠F1PF2=90°,求得x2+y2的值,进而根据2xy= -(x-y)
-(x-y)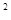 求得xy,进而可求得∴△F1PF2的面积. 解:设|PF1|=x,|PF2|=y,(x>y),根据双曲线性质可知x-y=4,∵∠F1PF2=90°,∴
求得xy,进而可求得∴△F1PF2的面积. 解:设|PF1|=x,|PF2|=y,(x>y),根据双曲线性质可知x-y=4,∵∠F1PF2=90°,∴ ,∴2xy=
,∴2xy= -(x-y)
-(x-y)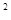 =4,∴xy=2,∴△F1PF2的面积为
=4,∴xy=2,∴△F1PF2的面积为 =1,故选A
=1,故选A
考点:双曲线的简单性质
点评:本题主要考查了双曲线的简单性质.要灵活运用双曲线的定义及焦距、实轴、虚轴等之间的关

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
曲线 +
+ =1.(m<6) 与
=1.(m<6) 与 +
+ =1.(5<m<9)的( )
=1.(5<m<9)的( )
| A.准线相同 | B.离心率相同 | C.焦点相同 | D.焦距相同 |
点 在直线
在直线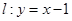 上,若存在过
上,若存在过 的直线交抛物线
的直线交抛物线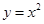 于
于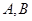 两点,且
两点,且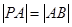 ,则称点
,则称点 为“
为“ 点”,那么下列结论中正确的是( )
点”,那么下列结论中正确的是( )
A.直线 上的所有点都是“ 上的所有点都是“ 点” 点” | B.直线 上仅有有限个点是“ 上仅有有限个点是“ 点” 点” |
C.直线 上的所有点都不是“ 上的所有点都不是“ 点” 点” | D.直线 上有无穷多个点是“ 上有无穷多个点是“ 点” 点” |
设双曲线 的焦点为F1、F2,过F1作x轴的垂线与该双曲线相交,其中一个交点为M,则|
的焦点为F1、F2,过F1作x轴的垂线与该双曲线相交,其中一个交点为M,则| |=
|=
A.5 | B.4 | C.3 | D.2 |
设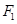 和
和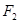 为双曲线
为双曲线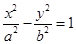 (
(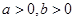 )的两个焦点, 若点
)的两个焦点, 若点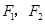 和点
和点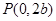 是正三角形的三个顶点,则双曲线的离心率为( )。
是正三角形的三个顶点,则双曲线的离心率为( )。
A.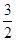 | B.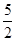 | C.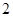 | D.3 |
抛物线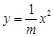 的焦点坐标为( )
的焦点坐标为( )
A.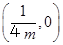 | B.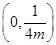 | C.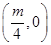 | D.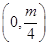 |
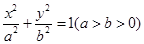 与双曲线
与双曲线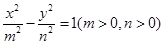 有相同的焦点
有相同的焦点 和
和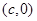 ,若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率为
,若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率为

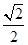
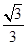
 相切倾斜角为
相切倾斜角为 的直线
的直线 与
与 轴和
轴和 轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线
轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线 C.2 D.
C.2 D. 和
和 为双曲线
为双曲线 (
( )的两个焦点, 若点
)的两个焦点, 若点 和点
和点 是正三角形的三个顶点,则双曲线的离心率为( )。
是正三角形的三个顶点,则双曲线的离心率为( )。

