Question

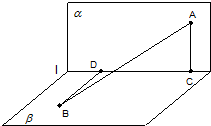
如图，长度为2的线段AB夹在直二面角α-l-β的两个半平面内，A∈α，B∈β，
且AB与平面α、β所成的角都是30°，AC⊥l，垂足为C，BD⊥l，垂足为D．
（Ⅰ）求直线AB与CD所成角的大小；
（Ⅱ）求二面角C-AB-D所成平面角的余弦值．

Answer 1

（Ⅰ）如图所示，连接BC，设直线AB与CD所成的角为θ，则由AC⊥β知：cosθ=cos∠ABC•cos∠DCB=cos30°•

2

3

=

2

2

，
故θ=45°；
（Ⅱ）如图建立空间直角坐标系，则D（0，0，0），A(0，

2

，1)，B（1，0，0），C(0，

2

，0)，
所以

CA

=(0，0，1)，

CB

=(1，-

2

，0)，设

n1

=(x，y，z)是平面ABC的法向量，则

CA • n1 =z=0 CB • n1 =x- 2 y=0

?可以取

n1

=(

2

，1，0)．
同理，

n2

=(0，1，-

2

)是平面ABD的法向量．
设二面角C-AB-D所成的平面角为γ，则显然γ是锐角，从而有cosγ=|

n1 • n2

| n1 |•| n2 |

|=

1

3 × 3

=

1

3

．