题目内容
13.已知圆O:x2+y2=1和直线l:x=3,在x轴上有一点Q(1,0),在圆O上有不与Q重合的两动点P、M,设直线MP斜率为k1,直线MQ斜率为k2,直线PQ斜率为k3.(1)若k1k2=-1
①求出点P的坐标;
②MP交l与P′,MQ交l与Q′.求证:以P′Q′为直径的圆,总过定点,并求出定点的坐标;
(2)若k2k3=2,判断直线PM是否经过定点,若有,求出来;若没有,请说明理由.
分析 (1)①k1k2=-1,可得PM⊥MQ,即PQ为直径,进而得到P的坐标;
②设M(m,n),P'(3,s),Q'(3,t),由三点共线,斜率相等,再由直径式圆的方程,结合恒过定点的思想,即可得到定点;
(2)运用特殊值,求出MP的两条直线方程,求得交点,再验证定点,由MP的方程代入圆的方程,运用韦达定理,再由直线的斜率公式,计算即可得到定值2,故定点成立.
解答 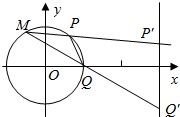 解:(1)①k1k2=-1,可得PM⊥MQ,
解:(1)①k1k2=-1,可得PM⊥MQ,
即有PQ为直径,即P的坐标为(-1,0);
②证明:设M(m,n),P'(3,s),Q'(3,t),
由P,M,P'共线,可得$\frac{n}{m+1}$=$\frac{s}{4}$,
由Q,M,Q'共线,可得$\frac{n}{m-1}$=$\frac{t}{2}$,
又m2+n2=1,即有n2=1-m2,
即有$\frac{st}{8}$=$\frac{{n}^{2}}{{m}^{2}-1}$=-1,即为st=-8,
以P′Q′为直径的圆的方程为(x-3)2+(y-s)(y-t)=0,
即有(x-3)2+y2+st-y(s+t)=0,
即(x-3)2+y2-8-y(s+t)=0,
不过s,t为何值,令y=0,(x-3)2+y2-8=0,
解得y=0,x=3±2$\sqrt{2}$.
则有以P′Q′为直径的圆,总过定点,定点的坐标为(3±2$\sqrt{2}$,0);
(2)k2k3=2,所以k2,k3同号.
不妨设k2=1,则QM:y=x-1,与圆的方程联立,解得M(0,-1),
k3=2,则QP:y=2(x-1),与圆的方程联立,解得P($\frac{3}{5}$,-$\frac{4}{5}$),此时MP:x-3y-3=0,
同理由圆的对称性,当M(0,-1)时,k2=-1,k3=-2,此时P(($\frac{3}{5}$,$\frac{4}{5}$),MP:x+3y-3=0,
若MP过定点,联立直线MP的方程,求得交点为(3,0),
验证:(3,0)是否为定点.
可设MP:y=k(x-3),代入圆x2+y2=1,可得(1+k2)x2-6k2x+9k2-1=0,
设M(x1,y1),P(x2,y2),即有x1+x2=$\frac{6{k}^{2}}{1+{k}^{2}}$,x1x2=$\frac{9{k}^{2}-1}{1+{k}^{2}}$,
则k2k3=$\frac{{y}_{1}}{{x}_{1}-1}$•$\frac{{y}_{2}}{{x}_{2}-1}$=$\frac{{k}^{2}({x}_{1}-3)({x}_{2}-3)}{({x}_{1}-1)({x}_{2}-1)}$
=$\frac{{k}^{2}({x}_{1}{x}_{2}+9-3({x}_{1}+{x}_{2}))}{{x}_{1}{x}_{2}+1-({x}_{1}+{x}_{2})}$,
代入韦达定理,化简可得k2k3=2.
则有直线PM经过定点(3,0).
点评 本题考查直线和圆的位置关系,考查直线方程和圆的方程的运用,以及直线斜率公式的运用,考查运算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | ?x0∈R,使得${e^{x_0}}≤0$ | B. | ?x∈R,x2+1<3x | ||
| C. | ?x0∈R,使得|x0-3|+|x0-1|<2 | D. | ?x>0,x+$\frac{4}{x}$≥4 |
| A. | $2-\sqrt{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{2}{3}$ |