题目内容
 如图,正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
如图,正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.(Ⅰ)求证:A1C∥平面AB1D;
(Ⅱ)求二面角B-AB1-D的正切值;
(Ⅲ)求点C到平面AB1D的距离.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)连接A1B,交AB1于E,连DE,由矩形的性质及三角形中位线定理,可得DE∥A1C,再由线面平行的判定定理,即可得到A1C∥平面AB1D.
(Ⅱ)过D作DF⊥AB于F,过F作FG⊥AB1于G,连接DG.我们可以得到∠DGF为二面角B-AB1-D的平面角.解三角形DGF,即可求出二面角B-AB1-D的正切值.
(Ⅲ)连接A1D,设点C到平面AB1D的距离为d.由VA1-AB1D=VB1-A1AD,利用等积法能求出点C到平面AB1D的距离.
(Ⅱ)过D作DF⊥AB于F,过F作FG⊥AB1于G,连接DG.我们可以得到∠DGF为二面角B-AB1-D的平面角.解三角形DGF,即可求出二面角B-AB1-D的正切值.
(Ⅲ)连接A1D,设点C到平面AB1D的距离为d.由VA1-AB1D=VB1-A1AD,利用等积法能求出点C到平面AB1D的距离.
解答:
(Ⅰ)证明:连结A1B,AB1,交于点E,则E是AB1中点,
连结DE,∵D是BC的中点,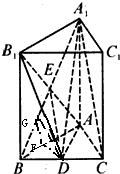
∴DE是△A1BC的中位线,
∴DE∥A1C,
∵A1C不包含于平面AB1D,DE?平面AB1D,
∴A1C∥平面AB1D.
(Ⅱ)过D作DF⊥AB于F,过F作FG⊥AB1于G,连接DG.
因为平面A1ABB1⊥平面ABC,DF⊥AB,所以DF⊥平面A1ABB1.
又AB1?平面A1ABB1,所以AB1⊥DF.
又FG⊥AB1,所以AB1⊥平面DFG,所以AB1⊥DG.
又AB1⊥FG,所以∠DGF为二面角B-AB1-D的平面角.
因为AA1=AB=1,
所以在正△ABC中,DF=
,
在△ABC中,FG=
BE=
,
所以在Rt△DFG中,tan∠DFG=
=
.
(Ⅲ)连接A1D,设点C到平面AB1D的距离为d.
因为正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1,
所以VA1-AB1D=VB1-A1AD,
所以
×
×
×
×d=
×
×
×1×1×
,
解得d=
.
故点C到平面AB1D的距离为
.
连结DE,∵D是BC的中点,

∴DE是△A1BC的中位线,
∴DE∥A1C,
∵A1C不包含于平面AB1D,DE?平面AB1D,
∴A1C∥平面AB1D.
(Ⅱ)过D作DF⊥AB于F,过F作FG⊥AB1于G,连接DG.
因为平面A1ABB1⊥平面ABC,DF⊥AB,所以DF⊥平面A1ABB1.
又AB1?平面A1ABB1,所以AB1⊥DF.
又FG⊥AB1,所以AB1⊥平面DFG,所以AB1⊥DG.
又AB1⊥FG,所以∠DGF为二面角B-AB1-D的平面角.
因为AA1=AB=1,
所以在正△ABC中,DF=
| ||
| 4 |
在△ABC中,FG=
| 3 |
| 4 |
3
| ||
| 8 |
所以在Rt△DFG中,tan∠DFG=
| DF |
| FG |
| ||
| 3 |
(Ⅲ)连接A1D,设点C到平面AB1D的距离为d.
因为正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1,
所以VA1-AB1D=VB1-A1AD,
所以
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
解得d=
| ||
| 5 |
故点C到平面AB1D的距离为
| ||
| 5 |
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面平行的判定,用空间向量求平面的夹角,解题时要注意空间思维能力的培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 叙述并证明面面垂直的性质定理.
叙述并证明面面垂直的性质定理. 如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3),求:
如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3),求: