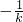题目内容
设f（x）是可导的奇函数，且f′（-x）=-k（k≠0），则f′（x）等于（ ）A．-k
B．k
C．
D．
【答案】分析：由f（x）是可导的奇函数，知其导函数f'（x）为偶函数，从而由f′（-x）=-k知f′（x）=-k．
解答：解：∵f（x）是可导的奇函数∴f（-x）=-f（x）
∴（f（-x））'=-f'（-x）=-f'（x）
∴f'（-x）=f'（x）
∴f'（x）是偶函数．
又∵f′（-x）=-k（k≠0）∴f′（x）=-k．
故选A．
点评：本题主要考查函数奇偶性的性质，同时考查了复合函数的求导法则，是个基础题．
解答：解：∵f（x）是可导的奇函数∴f（-x）=-f（x）
∴（f（-x））'=-f'（-x）=-f'（x）
∴f'（-x）=f'（x）
∴f'（x）是偶函数．
又∵f′（-x）=-k（k≠0）∴f′（x）=-k．
故选A．
点评：本题主要考查函数奇偶性的性质，同时考查了复合函数的求导法则，是个基础题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
设f（x）是可导的奇函数，且f′（-x0）=-k（k≠0），则f′（x0）等于（ ）
| A、-k | ||
| B、k | ||
C、
| ||
D、-
|
