题目内容
已知椭圆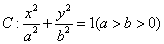 的离心率为
的离心率为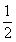 ,且过点
,且过点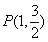 ,
,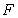 为其右焦点.
为其右焦点.
(1)求椭圆C的方程;
(2)设过点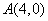 的直线
的直线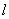 与椭圆相交于
与椭圆相交于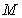 、
、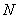 两点(点
两点(点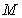 在
在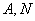 两点之间),若
两点之间),若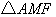 与
与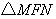 的面积相等,试求直线
的面积相等,试求直线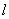 的方程.
的方程.
(1) ;(2)
;(2) 。
。
试题分析:(1)因为 ,所以
,所以 ,
, .
.
设椭圆方程为 ,又点
,又点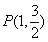 在椭圆上,所以
在椭圆上,所以 ,
,
解得 ,
,
所以椭圆方程为 .
.
(2)易知直线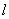 的斜率存在,
的斜率存在,
设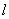 的方程为
的方程为 , 由
, 由 消去
消去 整理,得
整理,得
 ,
,
由题意知 ,
,
解得 .
.
设 ,
, ,则
,则 , ①,
, ①,  . ②.
. ②.
因为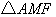 与
与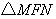 的面积相等,
的面积相等,
所以 ,所以
,所以 . ③ 由①③消去
. ③ 由①③消去 得
得 . ④
. ④
将 代入②得
代入②得 . ⑤
. ⑤
将④代入⑤ ,
,
整理化简得 ,解得
,解得 ,经检验成立.
,经检验成立.
所以直线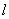 的方程为
的方程为 .
.

练习册系列答案
相关题目
 绕坐标原点按逆时针方向旋转45°,求所得曲线的方程.
绕坐标原点按逆时针方向旋转45°,求所得曲线的方程. ,
, ,且
,且 ,则
,则 的值是 .
的值是 . )的x的取值范围是( )
)的x的取值范围是( )  B.
B. C.
C. D.
D.
 , 则
, 则 的最大值是________________;
的最大值是________________;
 在x=1处取到极值,则a的值为( )
在x=1处取到极值,则a的值为( )
 B.
B.
 C.0 D.
C.0 D.


 ,若
,若
 是奇函数,则曲线
是奇函数,则曲线
 在点
在点
 处的切线方程是( )
处的切线方程是( )
 B.
B.

 D.
D.
 的直角坐标为
的直角坐标为 ,则点
,则点 B.
B.  C.
C. D.
D.
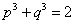 ,求证:
,求证: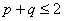 .用反证法证明时,可假设
.用反证法证明时,可假设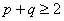 ;
;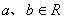 ,
,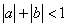 ,求证:方程
,求证:方程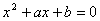 的两根的绝对值都小于1.用反证法证明时可假设方程有一根
的两根的绝对值都小于1.用反证法证明时可假设方程有一根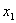 的绝对值大于或等于1,即假设
的绝对值大于或等于1,即假设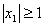 ;
;